 por Jhenrique » Qua Set 26, 2012 19:09
por Jhenrique » Qua Set 26, 2012 19:09
Quando definimos a seguinte função
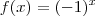
ela pode ser interpretada visualmente assim

, ou seja, eu sei explicitamente o que acontece se o x variar, porque a parte real é

e a parte imaginária é
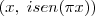
.
Agora, se uma função polinomial do 2º grau chamada

, por exemplo, gera um número complexo
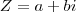
eu não sei o que isso significa. Eu não sei o que acontece caso eu variar o

... não sei se o termo

varia na mesma proporção.. e somar

tem algum significado... o que acontece se eu variar o

, o

varia na mesma proporção, ou o

ou nenhum dos dois??????
Não consigo fazer essas experiências empíricas no GeoGebra. MUITO do que eu aprendi sobre função foi graças ao GeoGebra. Mas ele não é um bom programa para funções complexas. Então não consigo compreendê-las.
PS: Abri um tópico na seção Numeros Complexos intitulado [Z=a+bi] Entendendo isso melhor para tratar extamente dessa dúvida e manter o fórum organizado."A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por Jhenrique » Sex Set 28, 2012 01:04
por Jhenrique » Sex Set 28, 2012 01:04
Pois bem, percebi que existem 2 maneira de descobrir a função polinomial que intersecta uma lista de pontos dados no plano xy. A primeira é pela interpolação de Lagrange e a segunda é através de sistema linear com os coeficientes do polinômio.
Inevitavelmente surgem 2 perguntas: (1) pra que existe a interpolação de Lagrange se os coeficientes dum polinomio podem ser descobertos por sistema linear?
(2) Qual é a formato padrão duma função exponencial?

? Porque sabendo do formato padrão da função exponencial, dado uma lista de pontos no plano xy, eu também poderia descobrir a expressão que intersecta esses pontos!

"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Sex Set 28, 2012 10:30
por MarceloFantini » Sex Set 28, 2012 10:30
Não sei as utilidades de interpolação de Lagrange, não posso te ajudar. A expressão padrão de uma exponencial é
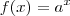
, com

e
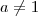
. A função que escreveu pode ser obtida por operações com outras funções, como composições e produtos.
dado uma lista de pontos no plano xy, eu também poderia descobrir a expressão que intersecta esses pontos!

Não é verdade. O que acontece é que você normalmente assume que é uma função contínua, que atende a certos padrões, etc, e vê que uma boa idéia é tentar aproximar por uma função exponencial. Mas dada uma lista de pontos arbitrária, a rigor não há qualquer forma de descobrir que função que é.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Dom Out 21, 2012 00:58
por Jhenrique » Dom Out 21, 2012 00:58
isso não é bem verdade, Marcelo.
Estive um tempo fora e também estudando, aprendi que podemos fazer um paralelo entre os coeficientes da função afim e os da exponencial:


então eu também gostaria de saber se este paralelo está correto:


"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Dom Out 21, 2012 01:14
por MarceloFantini » Dom Out 21, 2012 01:14
O que não é bem verdade? Também não consigo entender que paralelos você diz ter traçado, pode detalhar um pouco mais suas idéias por trás destas funções?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Seg Out 22, 2012 21:52
por Jhenrique » Seg Out 22, 2012 21:52
Quando eu te perguntei se a função exponencial assumia outra representação, vc me afirmou que ela é como a definição é (
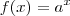
).
Mas ela pode ser expressa como

Sendo o coeficiente

a taxa de variação e o coeficiente

o valor inicial.
Ou seja, os coeficientes da função exponencial assumem os mesmos conceitos dos coeficiente da função afim

.
Ou seja, isso também dá a noção que para definir uma função exponencial de grau 1 no plano é necessário no mínimo dois pontos.
Outra coisa importante que eu aprendi é que
toda sequência é uma função com o domínio restrito no conjunto dos Naturais.
Ora, se existe uma função de segunda ordem para a função afim (

) então também existe uma função de segunda ordem para a função exponencial (

seria esta a expressão?).
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Ter Out 23, 2012 00:22
por MarceloFantini » Ter Out 23, 2012 00:22
A única representação da função exponencial é
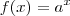
. A função que você disse pode ser obtida através de operações com funções, tomando
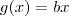
e
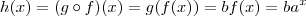
, ou mesmo

e
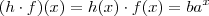
.
Cuidado ao dizer que assumem os mesmos coeficientes. Tem significados completamente diferentes e simplesmente usar a mesma letra para denotar não resolve isto.
É possível definir uma curva exponencial passando por dois pontos, o que não garante nada se você tiver três pontos ou mais. Por isso existem aproximações.
Sim, esta é a definição de sequência.
Este seu termo "existe uma função de segunda ordem para a função afim" não faz sentido. Funções não tem ordens. Uma função afim é um polinômio de grau 1, uma parábola é um polinômio de grau 2. De qualquer forma, qual seria o seu propósito com uma expressão do tipo

. Novamente, perceba que pode ser obtida por operações com as funções

,
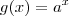
,

,
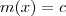
. Faça

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Ter Out 23, 2012 19:18
por Jhenrique » Ter Out 23, 2012 19:18
Vou perguntar mais uma vez...
Se

é uma função característica duma PA de 1ª ordem e
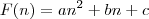
duma de 2ª.
Então, como é a função característica duma PG de 2ª ordem, sabendo que a de 1ª é

?
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Ter Out 23, 2012 22:40
por MarceloFantini » Ter Out 23, 2012 22:40
Não sei. Defina uma P.G. de segunda ordem. Quais são suas propriedades? De onde ela surge? Se você quer usar raciocínio análogo ao da P.A. de primeira e segunda ordens, primeiro precisa encontrar uma expressão equivalente para uma P.G., no caso uma sequência cuja diferença de termos seja uma P.G..
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Qua Out 24, 2012 10:37
por Jhenrique » Qua Out 24, 2012 10:37
Eu entendo como PG de 2ª ordem uma sequência cuja a razão entre termos consecutivos não é uma constante e sim uma progressão geométrica.
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Qua Out 24, 2012 19:04
por MarceloFantini » Qua Out 24, 2012 19:04
Então construa uma sequência que não esteja em progressão geométrica mas cuja razão esteja. Faça as contas e veja no que chega, é melhor do que conjecturar uma possível expressão.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Qua Out 24, 2012 20:08
por Jhenrique » Qua Out 24, 2012 20:08
Eu já fiz isso, basta eu integrar a função exponencial e o resultado é uma PG de 2ª ordem, se é que existe isso rs.
Mas a definição algébrica é sempre superior aos cálculos aritméticos, por isso vim aqui perguntar sobre o assunto e por detalhes.
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Qua Out 24, 2012 20:34
por MarceloFantini » Qua Out 24, 2012 20:34
Você tomou uma sequência

,

e assim em diante? Mostre suas contas, elas não fazem sentido para mim. Qual o propósito de integrar uma função exponencial? Onde está a sequência e a relação encontrada a partir dela, como disse? Além do mais, a definição algébrica é posterior aos cálculos aritméticos.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Sex Out 26, 2012 00:30
por Jhenrique » Sex Out 26, 2012 00:30
Eu me enganei! Pensei que integrando uma PG obteria uma PG de 2ª ordem, mas não é isso que acontece.
Agora eu cheguei uma conclusão importante... o cálculo diferencial e integral é desenvolvido para funções aritméticas e não para geométricas? Porque a derivação, que é a taxa de variação, é definida como a razão duma diferença pela outra, mas para uma função expoencial a taxa de variação não deveria ser a raiz duma razão pela outra?
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Sex Out 26, 2012 00:55
por MarceloFantini » Sex Out 26, 2012 00:55
Agora eu cheguei uma conclusão importante... o cálculo diferencial e integral é desenvolvido para funções aritméticas e não para geométricas? Porque a derivação, que é a taxa de variação, é definida como a razão duma diferença pela outra, mas para uma função expoencial a taxa de variação não deveria ser a raiz duma razão pela outra?
O que você quer dizer com funções aritméticas e geométricas? Derivação e integração valem para funções que são contínuas, pelo menos. Se não há continuidade, não podem existir essas operações. Além disso, o conceito de taxa de variação não muda de uma função para a outra.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Sex Out 26, 2012 10:48
por Jhenrique » Sex Out 26, 2012 10:48
O que eu quis dizer com função aritmética é função polinomial e o que eu quis dizer com função geométrica é função exponencial.
Sobre o conceito de taxa de variação e derivação, eu já havia pensado nisso antes. Para certo tipos de contas ou equações, os conceitos de Somatório, de média aritmética e de taxa de variação caem como uma luva. Por outro lado, para certo tipo de contas ou equações, os conceitos que fazem sentido são o de Produtório, média geométrica, entre outros...
Existe Progressão Geométrica de 2ª ordem, eu já achei conteúdo sobre isso, como já achei conteúdo de progressões mistas também, porém, as explicações estão sempre em formato de sequências (eu não suporto isso!), mas eu quero compreender o assunto de modo que eu possa relacioná-lo com funções exponenciais, por n motivos.
Um dos n motivos é a oportunidade de integrar e de derivar. Eu já tentei isso, integrei, mas a primitiva da função exponencial não era a exponencial de 2ª ordem que eu buscava. Compreende meu raciocínio e aonde quero chegar?
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Sex Out 26, 2012 11:29
por MarceloFantini » Sex Out 26, 2012 11:29
Não entendo porque não suporta sequências gerais, elas são muito mais interessantes e úteis que progressões aritméticas e geométricas no geral. Geométricas são uma classe particular bem interessante, porém aritméticas não. Se você entender sequências, é provável que consiga fazer o salto que quer.
Certo, existem conceitos adequados a cada tipo de análise. Qual é o seu ponto? Os exemplos que deu são simplesmente traduções de conceito de uma operação para outra.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Sex Out 26, 2012 11:39
por Jhenrique » Sex Out 26, 2012 11:39
Ah, é que, para mim, trabalhar com funções é bem mais intuitivo do que trabalhar com aquelas longas sequências e deduções.
O ponto que eu quero chegar é o seguinte. Quero aplicar algum tipo de cálculo (que não é o diferencial e o integral que conhecemos) numa função exponencial e obter tanto o gráfico quanto a expressão de 2ª ordem.
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Sex Out 26, 2012 11:49
por MarceloFantini » Sex Out 26, 2012 11:49
Uma sequência é uma função, onde está sua intuição? Sobre o que quer fazer, não sei.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Qua Out 31, 2012 18:39
por Jhenrique » Qua Out 31, 2012 18:39
Mas eu descobri.
A Função primitiva
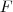
da função
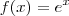
é
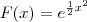
. Basta aplica o limite abaixo na função primitiva e o resultado será a sua derivada.
![\lim_{h->0} \sqrt[h]{\frac{f(x+h)}{f(x)}} \lim_{h->0} \sqrt[h]{\frac{f(x+h)}{f(x)}}](/latexrender/pictures/773323a5adaddee9b66b2f8819194e95.png)
Ademais, para mim não faz sentido que a derivada de

é

.

cresce geometricamente, portanto, creio que o limite que deve ser aplicado é o limite acima, citado por mim, e a sua derivada será a constante

.
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Qua Out 31, 2012 19:11
por MarceloFantini » Qua Out 31, 2012 19:11
Então você nega a interpretação da derivada de uma função real como o coeficiente angular da reta tangente ou está dizendo que a reta tangente à curva
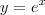
tem coeficiente angular constante, ou seja, é uma reta.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Qua Out 31, 2012 19:42
por Jhenrique » Qua Out 31, 2012 19:42
MarceloFantini escreveu:Então você nega a interpretação da derivada de uma função real como o coeficiente angular da reta tangente ou está dizendo que a reta tangente à curva
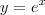
tem coeficiente angular constante, ou seja, é uma reta.
Sim, estou dizendo que "a reta tangente à curva
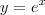
tem coeficiente angular constante, ou seja, é uma reta".
Basta plotar tal função num gráfico com o eixo X graduado como f(n)=1n e com o eixo Y graduado como f(n)=e^n e verá que é uma reta sim. Digo que a interpretação duma função exponencial exige outra perspectiva. Digo que as funções exponenciais são do tipo geométrica, portanto, a tx de variação é uma razão, e ñ uma diferença, logo, basta tomar
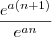
e o resultado será

. O coeficiente

é inclinação dessa reta.
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Qua Out 31, 2012 19:50
por MarceloFantini » Qua Out 31, 2012 19:50
Se

, o que você está fazendo é impossível. Não existe continuidade em conjuntos como os naturais ou os inteiros.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Relação entre funções com derivadas iguais
por matmatco » Sex Abr 12, 2013 23:00
- 8 Respostas
- 6423 Exibições
- Última mensagem por matmatco

Dom Abr 14, 2013 19:52
Cálculo: Limites, Derivadas e Integrais
-
- Relação entre cordas entre dois pontos de retas.
por janderson77 » Seg Dez 02, 2013 12:00
- 0 Respostas
- 2056 Exibições
- Última mensagem por janderson77

Seg Dez 02, 2013 12:00
Trigonometria
-
- relação entre x e y
por Apotema » Qua Nov 18, 2009 19:57
- 4 Respostas
- 5860 Exibições
- Última mensagem por Apotema

Seg Nov 23, 2009 08:12
Trigonometria
-
- relação entre a e b
por jose henrique » Seg Set 13, 2010 09:31
- 3 Respostas
- 4712 Exibições
- Última mensagem por Elcioschin

Ter Set 14, 2010 10:45
Álgebra Elementar
-
- [relação entre PA e PG]
por JKS » Qui Abr 11, 2013 01:11
- 2 Respostas
- 3480 Exibições
- Última mensagem por JKS

Dom Abr 21, 2013 18:07
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
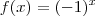 ela pode ser interpretada visualmente assim
ela pode ser interpretada visualmente assim  , ou seja, eu sei explicitamente o que acontece se o x variar, porque a parte real é
, ou seja, eu sei explicitamente o que acontece se o x variar, porque a parte real é  e a parte imaginária é
e a parte imaginária é 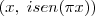 .
. , por exemplo, gera um número complexo
, por exemplo, gera um número complexo 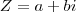 eu não sei o que isso significa. Eu não sei o que acontece caso eu variar o
eu não sei o que isso significa. Eu não sei o que acontece caso eu variar o  ... não sei se o termo
... não sei se o termo  varia na mesma proporção.. e somar
varia na mesma proporção.. e somar  tem algum significado... o que acontece se eu variar o
tem algum significado... o que acontece se eu variar o  , o
, o  varia na mesma proporção, ou o
varia na mesma proporção, ou o  ou nenhum dos dois??????
ou nenhum dos dois??????

 ? Porque sabendo do formato padrão da função exponencial, dado uma lista de pontos no plano xy, eu também poderia descobrir a expressão que intersecta esses pontos!
? Porque sabendo do formato padrão da função exponencial, dado uma lista de pontos no plano xy, eu também poderia descobrir a expressão que intersecta esses pontos! 
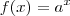 , com
, com  e
e 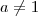 . A função que escreveu pode ser obtida por operações com outras funções, como composições e produtos.
. A função que escreveu pode ser obtida por operações com outras funções, como composições e produtos.





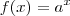 ).
).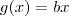 e
e 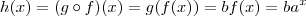 , ou mesmo
, ou mesmo  e
e 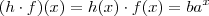 .
. . Novamente, perceba que pode ser obtida por operações com as funções
. Novamente, perceba que pode ser obtida por operações com as funções  ,
, 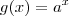 ,
,  ,
, 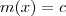 . Faça
. Faça  .
. é uma função característica duma PA de 1ª ordem e
é uma função característica duma PA de 1ª ordem e 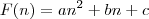 duma de 2ª.
duma de 2ª. ?
? ,
,  e assim em diante? Mostre suas contas, elas não fazem sentido para mim. Qual o propósito de integrar uma função exponencial? Onde está a sequência e a relação encontrada a partir dela, como disse? Além do mais, a definição algébrica é posterior aos cálculos aritméticos.
e assim em diante? Mostre suas contas, elas não fazem sentido para mim. Qual o propósito de integrar uma função exponencial? Onde está a sequência e a relação encontrada a partir dela, como disse? Além do mais, a definição algébrica é posterior aos cálculos aritméticos.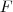 da função
da função 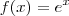 é
é 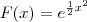 . Basta aplica o limite abaixo na função primitiva e o resultado será a sua derivada.
. Basta aplica o limite abaixo na função primitiva e o resultado será a sua derivada.![\lim_{h->0} \sqrt[h]{\frac{f(x+h)}{f(x)}} \lim_{h->0} \sqrt[h]{\frac{f(x+h)}{f(x)}}](/latexrender/pictures/773323a5adaddee9b66b2f8819194e95.png)
 é
é  .
.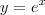 tem coeficiente angular constante, ou seja, é uma reta.
tem coeficiente angular constante, ou seja, é uma reta.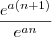 e o resultado será
e o resultado será  . O coeficiente
. O coeficiente  , o que você está fazendo é impossível. Não existe continuidade em conjuntos como os naturais ou os inteiros.
, o que você está fazendo é impossível. Não existe continuidade em conjuntos como os naturais ou os inteiros.




