Um tanque tem a forma de um cone invertido com 16m de altura e uma base com 4m de raio. A água "flui" no tanque a uma taxa de
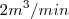 . Com que velocidade o nível da água estará se elevando quando sua profundidade for de 5m?
. Com que velocidade o nível da água estará se elevando quando sua profundidade for de 5m?Tentei fazer da seguinte forma:
Como não sei a fórmula do cálculo do volume de um cone, pesquisei na internet e obtive

Interpretando o enunciado, sei que
 e eu quero
e eu quero  .
.Mesmo que com uma certa incerteza, cheguei na seguinte conclusão:

Como podem ver, a função
 está em função de r(raio) e h(altura), então por semelhança de triângulos, fiz o seguinte:
está em função de r(raio) e h(altura), então por semelhança de triângulos, fiz o seguinte: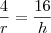

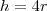
substituindo na função e arrumando, temos:
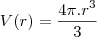
Derivando:

Substituindo em


 quando h=5, =
quando h=5, = 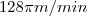
No gabarito, o resultado deveria ser
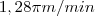 .
.Se forem perceber, nem usei a informação da profundidade de 5m e acredito que meu erro está relacionado a isto...
Qual foi o meu erro?
Edit:
Me desculpe gente, fiquei fuçando no exercício e acabei copiando errado aqui...
na verdade pra dar tal resultado que deu, primeiramente eu havia feito a seguinte relação:
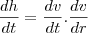



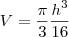

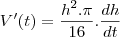
 e h=5 voce encontra
e h=5 voce encontra 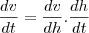

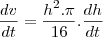

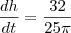

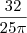 mas o gabarito deu
mas o gabarito deu  . Não são diferentes?
. Não são diferentes?