santhiago escreveu:Tome cuidado com ii) . Não necessariamente

. Contra exemplo , vamos supor que
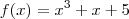
.É fácil ver que
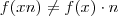
pois ,

.
Ah, então, não te respondi antes pq estava ocupado, mas já estudei o assunto.
Realmente, seu contra-exemplo está certo. Porém, a função que vc usou não satisfaz nenhuma das igualdades proporcionais abaixo.
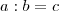
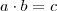


*Sendo

e

as váriveis e

a constante de proporcionalidade.
A função que vc citou não é uma proporção, não porque ela é do 2º grau, mas sim porque não é possível isolar as variáveis no 1º mebro e as constantes no 2º membro.
Eu até lanço a seguinte reflexão e questionamento: o requisito algébrico para grandezas serem proporcionais, é satisfazer uma das quatro equações acima, ok. Mas supondo

é a variável

, se

for

,

,
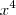
ou

, todas as propriedades de proporcionalidade continua sendo válidas, independente do expoente da variável

, fato.


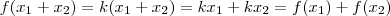
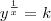






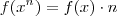



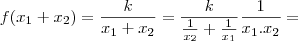

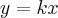



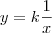

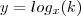
 . Contra exemplo , vamos supor que
. Contra exemplo , vamos supor que 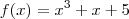 .É fácil ver que
.É fácil ver que 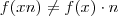 pois ,
pois ,  .
.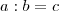
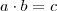


 e
e  as váriveis e
as váriveis e  a constante de proporcionalidade.
a constante de proporcionalidade. , se
, se  ,
,  ,
, 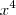 ou
ou  , todas as propriedades de proporcionalidade continua sendo válidas, independente do expoente da variável
, todas as propriedades de proporcionalidade continua sendo válidas, independente do expoente da variável  em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.