 por Jhenrique » Seg Out 15, 2012 13:13
por Jhenrique » Seg Out 15, 2012 13:13
Saudações, caros estudantes!
Farei algumas afirmações e gostaria que as confirmassem como verdadeiras ou não, a final de contas, posso ter deduzido algo errado...
Grandezas Diretamente Proporcionais
(i)

(ii)

(iii)
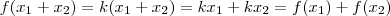
Do tipo Expononencial
(i)
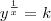
(ii)

(iii)

Grandezas Inversamente Proporcionais
(i)

(ii)

(iii)

Do tipo logarítmica
(i)

(ii)
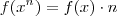
(iii)

Estão corretas?
Obg!
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por young_jedi » Seg Out 15, 2012 15:35
por young_jedi » Seg Out 15, 2012 15:35
verifiquei um equivoco, no tipo inversamente proporcional item III
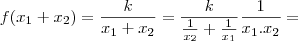

como voce pode ver o resultado é diferente
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Jhenrique » Sáb Out 20, 2012 23:37
por Jhenrique » Sáb Out 20, 2012 23:37
Tá tudo errado!
Vou redefinir os conceitos a fim de que se alguém pesquisar o assunto no fórum, que fique bem informado!
• Grandezas diretamente proporcionais
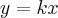
sua simétrica

do tipo exponencial

sua simétrica

• Grandezas inversamente proporcionais
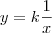
sua simétrica
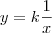
do tipo exponencial

sua simétrica
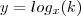
o resto é consequência dessas definições...
Jedi, vlw pelo alerta!
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por e8group » Sáb Out 20, 2012 23:49
por e8group » Sáb Out 20, 2012 23:49
Tome cuidado com ii) . Não necessariamente

. Contra exemplo , vamos supor que
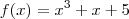
.É fácil ver que
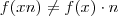
pois ,

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhenrique » Seg Nov 05, 2012 13:55
por Jhenrique » Seg Nov 05, 2012 13:55
santhiago escreveu:Tome cuidado com ii) . Não necessariamente

. Contra exemplo , vamos supor que
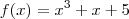
.É fácil ver que
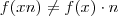
pois ,

.
Ah, então, não te respondi antes pq estava ocupado, mas já estudei o assunto.
Realmente, seu contra-exemplo está certo. Porém, a função que vc usou não satisfaz nenhuma das igualdades proporcionais abaixo.
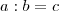
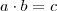


*Sendo

e

as váriveis e

a constante de proporcionalidade.
A função que vc citou não é uma proporção, não porque ela é do 2º grau, mas sim porque não é possível isolar as variáveis no 1º mebro e as constantes no 2º membro.
Eu até lanço a seguinte reflexão e questionamento: o requisito algébrico para grandezas serem proporcionais, é satisfazer uma das quatro equações acima, ok. Mas supondo

é a variável

, se

for

,

,
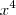
ou

, todas as propriedades de proporcionalidade continua sendo válidas, independente do expoente da variável

, fato.
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- grandezas inversamente porporcionais, me ajudem!!!!!!!
por zig » Dom Jun 26, 2011 20:50
- 2 Respostas
- 2510 Exibições
- Última mensagem por jrmatematico

Dom Mai 13, 2012 10:03
Sistemas de Equações
-
- Grandezas Proporcionais - Preciso de ajuda urgente!!!
por mark_adm » Sáb Mai 12, 2012 22:13
- 5 Respostas
- 3097 Exibições
- Última mensagem por geraldo

Seg Mai 14, 2012 12:33
Matemática Financeira
-
- diretamente proporcional
por dandara » Sex Abr 22, 2016 12:49
- 2 Respostas
- 2219 Exibições
- Última mensagem por dandara

Dom Abr 24, 2016 10:14
Aritmética
-
- Divisão Inversamente proporcional.
por Wizard » Dom Jan 01, 2012 20:27
- 2 Respostas
- 3928 Exibições
- Última mensagem por Wizard

Sex Jan 06, 2012 01:47
Tópicos sem Interação (leia as regras)
-
- Relação entre Grandezas
por Jhenrique » Sex Nov 16, 2012 02:49
- 3 Respostas
- 2887 Exibições
- Última mensagem por LuizAquino

Seg Nov 19, 2012 10:27
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


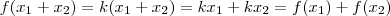
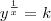






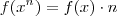



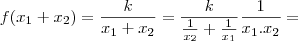

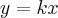



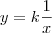

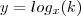
 . Contra exemplo , vamos supor que
. Contra exemplo , vamos supor que 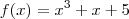 .É fácil ver que
.É fácil ver que 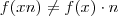 pois ,
pois ,  .
.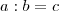
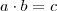


 e
e  as váriveis e
as váriveis e  a constante de proporcionalidade.
a constante de proporcionalidade. , se
, se  ,
,  ,
, 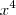 ou
ou  , todas as propriedades de proporcionalidade continua sendo válidas, independente do expoente da variável
, todas as propriedades de proporcionalidade continua sendo válidas, independente do expoente da variável