Ai vai
1) Resolva a inequação:

2) Estude a variação do sinal da função y=(x+3) ² - (x-2) ².
____________________________________
Tentei fazer a numero 1 e gostaria de opiniao de vcs..
separarei A e B pra ficar mais facil de me expressar
1)A:
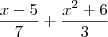 < B:
< B: 
A -
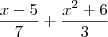 MMC 7,3 = 21
MMC 7,3 = 21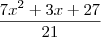
B -
 MMC 2,6,1 = 6
MMC 2,6,1 = 6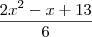
juntando novamente

dai tirei outrro MMC 21,6 = 42
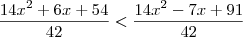
Cancelei o 42
14x²+6x+54< 14x²-7x+91
14x²-14x² +6x+7x < 91-54
13x < 37
x < 37/13 ou x < 2,846
__________________________________
A numero 2 eu nao faço a minima ideia de como faz..o que eu fiz foi no chute mesmo, certamente está errada
2) y = (x+3)² - (x-2)²
0 = (x²+6x+9) - (x²-4x+4)
0 = x²+6x+9 -x²+4x-4
0 = 10x+5
10x = -5
x =

imagino que esteja completamente errada...gostaria da ajuda de vcs em ambas questões...
Obrigado


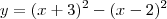




![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.