 por gabriel feron » Sex Set 28, 2012 02:41
por gabriel feron » Sex Set 28, 2012 02:41
seja f(x)=x²-3x. Encontre

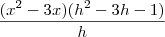
o que falta? estou certo?? a partir do primeiro igual fui eu que fiz...
obrigado!
-
gabriel feron
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Seg Abr 16, 2012 03:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Hídrica
- Andamento: cursando
 por Jhenrique » Sex Set 28, 2012 02:57
por Jhenrique » Sex Set 28, 2012 02:57
Segundo a definição de derivação, o

não é uma variável, é apenas um artifício algébrico para cálcular a função derivada da

.
Você quer o passo a passo?
Porque aplicando algumas propriedades de derivação
![[f(x)+g(x)]'=f'(x)+g'(x) [f(x)+g(x)]'=f'(x)+g'(x)](/latexrender/pictures/42d4692b5412eda2775446cd6ee1cf4b.png)
![[k\cdot f(x)]'=k\cdot[f(x)]' [k\cdot f(x)]'=k\cdot[f(x)]'](/latexrender/pictures/a35e7df96d78ada8a1eae6152fbf1e37.png)
É fácil cálcular que
![f'(x)=[x^2]'+[-3x]'=2x-3 f'(x)=[x^2]'+[-3x]'=2x-3](/latexrender/pictures/9161a9a0e54fc21f7d85efdf9fcc45fb.png)
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por gabriel feron » Sex Set 28, 2012 03:13
por gabriel feron » Sex Set 28, 2012 03:13
realmente dessa forma da pra se chegar facilmente ao resultado, tenho uma noção boa de derivada, mas não optei por utilizar a derivação, pois a questão encontra-se em um material de limites, e estou revisando o material separadamente, já que minha faculdade retorna da greve na próxima semana... mesmo assim valeuuuu!!

-
gabriel feron
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Seg Abr 16, 2012 03:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Hídrica
- Andamento: cursando
 por gabriel feron » Dom Set 30, 2012 19:58
por gabriel feron » Dom Set 30, 2012 19:58
MarceloFantini escreveu:Isto não é verdade. Note que
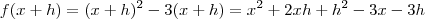
, assim
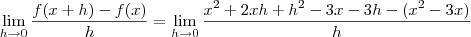
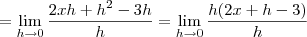

.
Exatamente isso, MUITO OBRIGADO MESMO!!

-
gabriel feron
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Seg Abr 16, 2012 03:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Hídrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite (1 variável)
por RenanDias » Sáb Out 26, 2013 22:49
- 2 Respostas
- 1240 Exibições
- Última mensagem por RenanDias

Seg Out 28, 2013 13:20
Cálculo: Limites, Derivadas e Integrais
-
- Limite simples com 1 variável
por RenanDias » Sáb Nov 02, 2013 19:47
- 0 Respostas
- 621 Exibições
- Última mensagem por RenanDias

Sáb Nov 02, 2013 19:47
Cálculo: Limites, Derivadas e Integrais
-
- Limite simples com 1 variável
por RenanDias » Sáb Nov 02, 2013 19:47
- 4 Respostas
- 1713 Exibições
- Última mensagem por RenanDias

Seg Nov 04, 2013 10:28
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6642 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4786 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

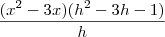


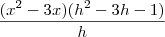

 não é uma variável, é apenas um artifício algébrico para cálcular a função derivada da
não é uma variável, é apenas um artifício algébrico para cálcular a função derivada da  .
.![[f(x)+g(x)]'=f'(x)+g'(x) [f(x)+g(x)]'=f'(x)+g'(x)](/latexrender/pictures/42d4692b5412eda2775446cd6ee1cf4b.png)
![[k\cdot f(x)]'=k\cdot[f(x)]' [k\cdot f(x)]'=k\cdot[f(x)]'](/latexrender/pictures/a35e7df96d78ada8a1eae6152fbf1e37.png)
![f'(x)=[x^2]'+[-3x]'=2x-3 f'(x)=[x^2]'+[-3x]'=2x-3](/latexrender/pictures/9161a9a0e54fc21f7d85efdf9fcc45fb.png)




, assim
.


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.