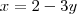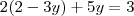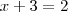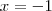por GABRIELA » Ter Set 01, 2009 17:17
por GABRIELA » Ter Set 01, 2009 17:17
A soma dos valores x e y que satisfazem a equação matricial

pelas minhas contas achei que fosse 1, mas a resposta é zero.Como calculo para achar a resposta
(desculpe, é pq estou aprendendo a mexer no editor de formulas.)

Está do jeito que coloquei as matrizes conf. o livro.
Editado pela última vez por
GABRIELA em Ter Set 01, 2009 20:19, em um total de 1 vez.
-
GABRIELA
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Seg Ago 31, 2009 17:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Ter Set 01, 2009 19:35
por Elcioschin » Ter Set 01, 2009 19:35
Gabriela
Não entendi a equação:
A primeira matriz é multiplicada ou somada com a segunda?
Pelo que entendí o problema pede DOIS valores: x e y. No entanto você afirma que a resposta é zero.
POr favor, esclareça, colocando o enunciado COMPLETO, inclusive com a resposta.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Molina » Ter Set 01, 2009 23:28
por Molina » Ter Set 01, 2009 23:28
GABRIELA escreveu:A soma dos valores x e y que satisfazem a equação matricial

pelas minhas contas achei que fosse 1, mas a resposta é zero.Como calculo para achar a resposta
(desculpe, é pq estou aprendendo a mexer no editor de formulas.)

Está do jeito que coloquei as matrizes conf. o livro.
Boa noite, Gabriela.
Fazendo a multiplicação de forma rotineira você irá chegar em um sistema:
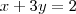
(equação 1)
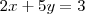
(equação 2)
Isolando x na equação 1 e substituindo na eq. 2, temos:
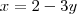
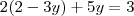



Substituindo y na eq. 1:
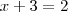
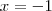
Logo:

Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvida em Questão de (EDO)
por sys_ » Sex Abr 10, 2009 19:06
- 2 Respostas
- 2317 Exibições
- Última mensagem por nakagumahissao

Seg Ago 17, 2015 13:04
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida em questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:18
- 3 Respostas
- 7250 Exibições
- Última mensagem por DanielFerreira

Dom Ago 23, 2009 12:59
Progressões
-
- duvida na questão
por GABRIELA » Qua Set 30, 2009 17:06
- 10 Respostas
- 6665 Exibições
- Última mensagem por GABRIELA

Qua Set 30, 2009 22:42
Geometria Analítica
-
- Dúvida em uma questão
por Padoan » Qua Ago 11, 2010 18:53
- 3 Respostas
- 3212 Exibições
- Última mensagem por Padoan

Sex Ago 13, 2010 23:10
Álgebra Elementar
-
- Duvida na questão
por igorcalfe » Qua Nov 03, 2010 16:21
- 2 Respostas
- 1634 Exibições
- Última mensagem por igorcalfe

Qua Nov 03, 2010 17:16
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.








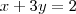 (equação 1)
(equação 1)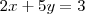 (equação 2)
(equação 2)