(FUVEST-SP) – Uma urna contém 20 bolas numeradas de 1 a 20. Seja o experimento: retirada de
uma bola. Considere os eventos: A = {a bola retirada possui um múltiplo de 2}; B = {a bola retirada
possui um múltiplo de 5}. Então, probabilidade do evento AUB é:
Achei p(A)=11/20, p(B)=1/4 e p(A intersecção B)= 11/80, como p(AUB)=p(A)+p(B)-p(A intersecção B), obtive resolvendo 53/80. Onde errei?


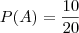 .
. .
. .
.
 é um número tal que, dividido por
é um número tal que, dividido por  deveria resultar um número inteiro. Mas isso não acontece, certo?
deveria resultar um número inteiro. Mas isso não acontece, certo?![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)