 por Ronaldobb » Qui Set 20, 2012 19:41
por Ronaldobb » Qui Set 20, 2012 19:41
Para o gráfico da função

mostrado abaixo.
http://i.imgur.com/gpEAJ.pnga) Determine o valor de

.
b) Encontre os valores de

para os quais

e
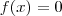
.
c) Determine o domínio de

d) Ache a imagem de

.
-
Ronaldobb
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Ter Set 18, 2012 19:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Ronaldobb » Qui Set 20, 2012 21:57
por Ronaldobb » Qui Set 20, 2012 21:57
Por favor explique como você encontrou

,

-
Ronaldobb
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Ter Set 18, 2012 19:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por MarceloFantini » Qui Set 20, 2012 22:01
por MarceloFantini » Qui Set 20, 2012 22:01
Você tentou algo?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Ronaldobb » Qui Set 20, 2012 22:07
por Ronaldobb » Qui Set 20, 2012 22:07
Aqui está a questão:
http://i.imgur.com/lHYRF.pngfiz um monte de contas pra achar as raízes. Sei que 1 é uma raíz, mas não sei a ou as outras raízes! Nem sei se é uma função quadrática ou um polinômio com mais raízes
-
Ronaldobb
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Ter Set 18, 2012 19:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por Ronaldobb » Qui Set 20, 2012 22:09
por Ronaldobb » Qui Set 20, 2012 22:09
Como achou o valor de

para

?
-
Ronaldobb
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Ter Set 18, 2012 19:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por MarceloFantini » Qui Set 20, 2012 22:13
por MarceloFantini » Qui Set 20, 2012 22:13
Use imagens apenas se absolutamente necessário, como gráficos. Todo ponto da função é um ponto do plano que pode ser descrito como
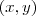
, mas em particular por ser função isso se torna

. Se vocÊ traçar uma reta vertical passando por

, verá que ela encontra a curva praticamente em

, logo

.
A questão não quer que você explicite a regra da função, e sim que saiba interpretar os conceitos.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Ronaldobb » Qui Set 20, 2012 22:34
por Ronaldobb » Qui Set 20, 2012 22:34
Obrigado. Deve ser isso mesmo. Pois a professora falou algo assim na aula
-
Ronaldobb
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Ter Set 18, 2012 19:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- questão cabulosa. Ajuda aqui!!!
por zenildo » Seg Mai 09, 2016 01:49
- 4 Respostas
- 3145 Exibições
- Última mensagem por zenildo

Qui Mai 12, 2016 22:43
Trigonometria
-
- Ajuda aqui com está função?
por Ronaldobb » Ter Set 18, 2012 19:56
- 2 Respostas
- 2546 Exibições
- Última mensagem por Russman

Ter Set 18, 2012 21:12
Funções
-
- Alguem me aquida aqui com essa derivada por favor?
por henr1ke001 » Seg Mai 28, 2012 12:01
- 1 Respostas
- 2059 Exibições
- Última mensagem por Max Cohen

Seg Mai 28, 2012 15:20
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda com essa questao, volume e area...
 por Anderson POntes » Sex Jul 09, 2010 01:24
por Anderson POntes » Sex Jul 09, 2010 01:24
- 2 Respostas
- 4335 Exibições
- Última mensagem por Anderson POntes

Sex Jul 09, 2010 01:59
Geometria Plana
-
- Preciso de ajuda com essa questão da Fundação Cesgranrio
por Jesicaa » Qui Mar 12, 2015 11:46
- 2 Respostas
- 3145 Exibições
- Última mensagem por Jesicaa

Dom Mar 15, 2015 00:06
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 mostrado abaixo.
mostrado abaixo. .
. para os quais
para os quais  e
e 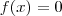 .
.
 .
.
 mostrado abaixo.
mostrado abaixo. .
. para os quais
para os quais  e
e 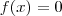 .
.
 .
.

 ,
,



 para
para  ?
?
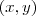 , mas em particular por ser função isso se torna
, mas em particular por ser função isso se torna  . Se vocÊ traçar uma reta vertical passando por
. Se vocÊ traçar uma reta vertical passando por  , verá que ela encontra a curva praticamente em
, verá que ela encontra a curva praticamente em  , logo
, logo  .
.

