![\sum_{n=1}^{\infty}\frac{\sqrt[]{n+2}}{2{n}^{2}+n+1} \sum_{n=1}^{\infty}\frac{\sqrt[]{n+2}}{2{n}^{2}+n+1}](/latexrender/pictures/f7aef64f474721cb5485cc43448512e8.png)
tentei fazer pelo testa da comparação no limite, comparei com a série
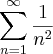 , mas acabei não consegui
, mas acabei não consegui
![\sum_{n=1}^{\infty}\frac{\sqrt[]{n+2}}{2{n}^{2}+n+1} \sum_{n=1}^{\infty}\frac{\sqrt[]{n+2}}{2{n}^{2}+n+1}](/latexrender/pictures/f7aef64f474721cb5485cc43448512e8.png)
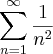 , mas acabei não consegui
, mas acabei não consegui


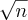 enquanto que a parte dominante no denominador é
enquanto que a parte dominante no denominador é  , então façamos:
, então façamos: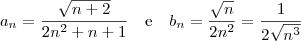
 e
e  sejam duas séries com termos positivos. Se
sejam duas séries com termos positivos. Se 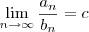
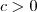 , então ambas as séries convergem ou ambas as séries divergem.
, então ambas as séries convergem ou ambas as séries divergem.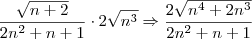
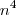 em evidência dentro da raiz e
em evidência dentro da raiz e  em evidência no denominador, teremos:
em evidência no denominador, teremos: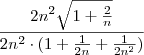
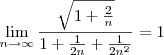
 é uma p-série com
é uma p-série com  , então
, então 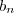 converge, e como c = 1 > 0 então a série dada converge pelo teste de Comparação no Limte....
converge, e como c = 1 > 0 então a série dada converge pelo teste de Comparação no Limte....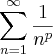 é convergente se
é convergente se 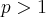 e divergente se
e divergente se  .
.

Guilherme Carvalho escreveu:Mas aqui no livro diz que a serie converge


Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.