 por Guilherme Carvalho » Seg Set 17, 2012 22:50
por Guilherme Carvalho » Seg Set 17, 2012 22:50
Não estou conseguindo descobrir se esta série converge ou não
![\sum_{n=1}^{\infty}\frac{\sqrt[]{n+2}}{2{n}^{2}+n+1} \sum_{n=1}^{\infty}\frac{\sqrt[]{n+2}}{2{n}^{2}+n+1}](/latexrender/pictures/f7aef64f474721cb5485cc43448512e8.png)
tentei fazer pelo testa da comparação no limite, comparei com a série
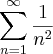
, mas acabei não consegui
-
Guilherme Carvalho
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Mar 03, 2011 12:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por MarceloFantini » Ter Set 18, 2012 00:38
por MarceloFantini » Ter Set 18, 2012 00:38
Segundo o
Wolfram ela converge, mas não faz os passos. Tentei várias vezes mas também não consegui.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Renato_RJ » Ter Set 18, 2012 03:03
por Renato_RJ » Ter Set 18, 2012 03:03
Boa noite amigos !!!
Eu acho que consegui provar que a série converge usando o teste de Comparação no Limite... Veja:
A parte dominante do numerador é
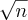
enquanto que a parte dominante no denominador é

, então façamos:
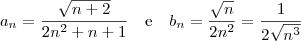
O teste de Comparação no Limte é enunciado da seguinte forma:
Suponha que

e

sejam duas séries com termos positivos. Se
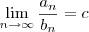
Onde c é um número finito e
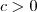
, então ambas as séries convergem ou ambas as séries divergem.
Então façamos:
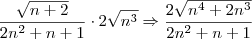
Colocando
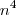
em evidência dentro da raiz e

em evidência no denominador, teremos:
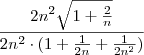
O que nos dá:
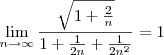
Como

é uma p-série com

, então
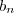
converge, e como c = 1 > 0 então a série dada converge pelo teste de Comparação no Limte....
Só para lembrar, uma p-série
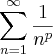
é convergente se
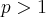
e divergente se

.
Espero que tudo esteja certo e que eu tenha ajudado...
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Guilherme Carvalho » Ter Set 18, 2012 15:15
por Guilherme Carvalho » Ter Set 18, 2012 15:15
Mas aqui no livro diz que a serie converge
-
Guilherme Carvalho
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Mar 03, 2011 12:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por Renato_RJ » Ter Set 18, 2012 15:18
por Renato_RJ » Ter Set 18, 2012 15:18
Guilherme Carvalho escreveu:Mas aqui no livro diz que a serie converge
Mas foi exatamente o que eu escrevi lá em cima.. A série dada converge pelo teste de Comparação do Limite....
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Guilherme Carvalho » Ter Set 18, 2012 16:24
por Guilherme Carvalho » Ter Set 18, 2012 16:24
Vdd li errado.....kkkkkkkkkk
-
Guilherme Carvalho
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Mar 03, 2011 12:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Séries] Sobre simplicação de expressões em séries
por HenriqueOrlan » Sáb Nov 21, 2015 11:28
- 1 Respostas
- 3726 Exibições
- Última mensagem por adauto martins

Qua Nov 25, 2015 16:31
Sequências
-
- Séries
por manuoliveira » Sex Mai 23, 2014 21:07
- 2 Respostas
- 2185 Exibições
- Última mensagem por Man Utd

Ter Mai 27, 2014 15:10
Sequências
-
- Sequencias e Séries
por Neperiano » Dom Set 26, 2010 19:28
- 1 Respostas
- 2257 Exibições
- Última mensagem por Marcampucio

Dom Set 26, 2010 21:36
Cálculo: Limites, Derivadas e Integrais
-
- Séries de pagamentos!
por Clara19 » Qua Abr 06, 2011 00:47
- 1 Respostas
- 2281 Exibições
- Última mensagem por Rogerio Murcila

Qua Mai 11, 2011 13:56
Matemática Financeira
-
- Series de Fourier
por 380625 » Qua Set 28, 2011 01:30
- 1 Respostas
- 1533 Exibições
- Última mensagem por Neperiano

Qua Set 28, 2011 15:21
Sequências
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sum_{n=1}^{\infty}\frac{\sqrt[]{n+2}}{2{n}^{2}+n+1} \sum_{n=1}^{\infty}\frac{\sqrt[]{n+2}}{2{n}^{2}+n+1}](/latexrender/pictures/f7aef64f474721cb5485cc43448512e8.png)
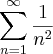 , mas acabei não consegui
, mas acabei não consegui
![\sum_{n=1}^{\infty}\frac{\sqrt[]{n+2}}{2{n}^{2}+n+1} \sum_{n=1}^{\infty}\frac{\sqrt[]{n+2}}{2{n}^{2}+n+1}](/latexrender/pictures/f7aef64f474721cb5485cc43448512e8.png)
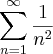 , mas acabei não consegui
, mas acabei não consegui


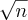 enquanto que a parte dominante no denominador é
enquanto que a parte dominante no denominador é  , então façamos:
, então façamos: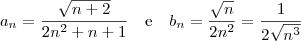
 e
e  sejam duas séries com termos positivos. Se
sejam duas séries com termos positivos. Se 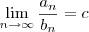
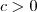 , então ambas as séries convergem ou ambas as séries divergem.
, então ambas as séries convergem ou ambas as séries divergem.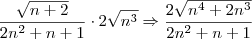
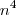 em evidência dentro da raiz e
em evidência dentro da raiz e  em evidência no denominador, teremos:
em evidência no denominador, teremos: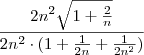
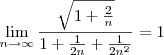
 é uma p-série com
é uma p-série com  , então
, então 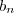 converge, e como c = 1 > 0 então a série dada converge pelo teste de Comparação no Limte....
converge, e como c = 1 > 0 então a série dada converge pelo teste de Comparação no Limte....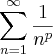 é convergente se
é convergente se 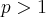 e divergente se
e divergente se  .
.








