 por iceman » Dom Set 16, 2012 23:06
por iceman » Dom Set 16, 2012 23:06

Não sei como faz essa.
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Seg Set 17, 2012 00:03
por MarceloFantini » Seg Set 17, 2012 00:03
Use a regra do quociente. Tome
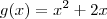
e

, então
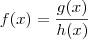
. A regra do quociente diz que
![f'(x) = \frac{g'(x) \cdot h(x) - g(x) \cdot h'(x)}{[h(x)]^2} f'(x) = \frac{g'(x) \cdot h(x) - g(x) \cdot h'(x)}{[h(x)]^2}](/latexrender/pictures/e20f378d5cc6a25d249a966a4578c59f.png)
.
Derive o que for necessário e substitua tudo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Russman » Seg Set 17, 2012 11:24
por Russman » Seg Set 17, 2012 11:24
Ou simplifique a função para

e derive usando a derivada de polinômios.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada - Questão
por iceman » Dom Set 16, 2012 16:37
- 3 Respostas
- 1716 Exibições
- Última mensagem por iceman

Dom Set 16, 2012 19:59
Cálculo: Limites, Derivadas e Integrais
-
- Derivada - Questão
por iceman » Ter Set 18, 2012 18:56
- 3 Respostas
- 1897 Exibições
- Última mensagem por Renato_RJ

Ter Set 18, 2012 19:24
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada Dy/Dx] Questão
por iceman » Sáb Nov 22, 2014 13:44
- 4 Respostas
- 1994 Exibições
- Última mensagem por adauto martins

Dom Nov 23, 2014 12:36
Cálculo: Limites, Derivadas e Integrais
-
- [DUVIDA] Questão de Derivada.
por Jefferson_mcz » Sex Mai 17, 2013 00:21
- 0 Respostas
- 1736 Exibições
- Última mensagem por Jefferson_mcz

Sex Mai 17, 2013 00:21
Cálculo: Limites, Derivadas e Integrais
-
- Derivada-questão da prova
por johnatta » Ter Jun 16, 2015 13:47
- 1 Respostas
- 2224 Exibições
- Última mensagem por DanielFerreira

Sáb Jun 27, 2015 15:57
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 Não sei como faz essa.
Não sei como faz essa.

 Não sei como faz essa.
Não sei como faz essa.
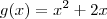 e
e  , então
, então 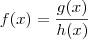 . A regra do quociente diz que
. A regra do quociente diz que![f'(x) = \frac{g'(x) \cdot h(x) - g(x) \cdot h'(x)}{[h(x)]^2} f'(x) = \frac{g'(x) \cdot h(x) - g(x) \cdot h'(x)}{[h(x)]^2}](/latexrender/pictures/e20f378d5cc6a25d249a966a4578c59f.png) .
.

 e derive usando a derivada de polinômios.
e derive usando a derivada de polinômios.

 .
.



