 por Alce » Qui Ago 23, 2012 14:09
por Alce » Qui Ago 23, 2012 14:09
Boa tarde, desenvolvi um modelo de planejamento de produção baseado na determinação do processo de custo mínimo como trabalho de conclusão de uma MBA em controladoria. Porém, o modelo de calculo que acabei desenvolvendo baseia-se em encontrar o valor de uma variável D que está em um expoente e me faltou conhecimento matemático para isolar a mesma na fórmula.
A formula é a seguinte:
LM(CE-CF)=CF(LM/2)x(1+i)^LM/D
Como ficaria esta formula isolando o D? Tipo D=...?
Ficaria muito grato se conseguisse alguma ajuda.
Grande abraço
-
Alce
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Ago 23, 2012 14:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Controladoria
- Andamento: formado
 por MarceloFantini » Qui Ago 23, 2012 16:22
por MarceloFantini » Qui Ago 23, 2012 16:22
Se a fórmula for

, então
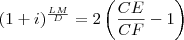
e daí

.
Finalmente,
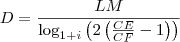
.
Não sei as restrições sobre

, mas devemos ter

e mais algumas condições para existência do logaritmo.
Editado: corrigindo um erro.
Editado pela última vez por
MarceloFantini em Qui Ago 23, 2012 17:12, em um total de 1 vez.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Alce » Qui Ago 23, 2012 16:56
por Alce » Qui Ago 23, 2012 16:56
Muito obrigado Marcelo, me forneceu uma grande ajuda. Confesso que ainda estou com dificuldade para executar a fórmula com a nova formatação em função do algorítimo. Se não fosse pedir muito, teria como me demonstrar a resolução da equação com valores reais? Segue os valores que utilizei no meu trabalho:
LM=180
CE=6
CF=5,36
i=1,5
Na fórmula:
180(6 - 5,36)=5,36(180/2)x(1+1,5)^180/D
Desde já agradeço...
-
Alce
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Ago 23, 2012 14:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Controladoria
- Andamento: formado
 por MarceloFantini » Qui Ago 23, 2012 17:16
por MarceloFantini » Qui Ago 23, 2012 17:16
A propósito, cometi um erro. O resultado final será
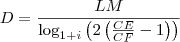
, pois

. Substituindo os valores, teremos:
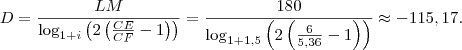
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Isolar Variável] Ajuda para isolar variável na equação
por Gabriel Gomes » Sex Fev 03, 2012 08:55
- 1 Respostas
- 10701 Exibições
- Última mensagem por MarceloFantini

Sáb Fev 04, 2012 12:51
Sistemas de Equações
-
- Isolar variável em Formula.
por viniciusbmello » Sex Jan 23, 2015 16:42
- 5 Respostas
- 4688 Exibições
- Última mensagem por viniciusbmello

Seg Jan 26, 2015 11:29
Equações
-
- [Isolar variável]Conclusão de exercício
por Bellamv » Ter Mai 14, 2013 03:29
- 0 Respostas
- 1327 Exibições
- Última mensagem por Bellamv

Ter Mai 14, 2013 03:29
Álgebra Elementar
-
- Isolar uma variável numa equação de grau 3
por KleinIll » Dom Abr 24, 2016 16:37
- 0 Respostas
- 7159 Exibições
- Última mensagem por KleinIll

Dom Abr 24, 2016 16:37
Equações
-
- Problema para isolar uma variável ---> "L"
por chenz » Sex Out 01, 2021 09:10
- 2 Respostas
- 8320 Exibições
- Última mensagem por chenz

Sáb Out 09, 2021 14:20
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , então
, então 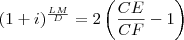
 .
.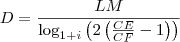 .
. , mas devemos ter
, mas devemos ter  e mais algumas condições para existência do logaritmo.
e mais algumas condições para existência do logaritmo.

 . Substituindo os valores, teremos:
. Substituindo os valores, teremos: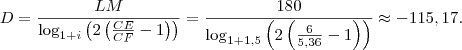
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.