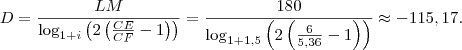por Alce » Qui Ago 23, 2012 14:09
por Alce » Qui Ago 23, 2012 14:09
Boa tarde, desenvolvi um modelo de planejamento de produção baseado na determinação do processo de custo mínimo como trabalho de conclusão de uma MBA em controladoria. Porém, o modelo de calculo que acabei desenvolvendo baseia-se em encontrar o valor de uma variável D que está em um expoente e me faltou conhecimento matemático para isolar a mesma na fórmula.
A formula é a seguinte:
LM(CE-CF)=CF(LM/2)x(1+i)^LM/D
Como ficaria esta formula isolando o D? Tipo D=...?
Ficaria muito grato se conseguisse alguma ajuda.
Grande abraço
-
Alce
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Ago 23, 2012 14:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Controladoria
- Andamento: formado
 por MarceloFantini » Qui Ago 23, 2012 16:22
por MarceloFantini » Qui Ago 23, 2012 16:22
Se a fórmula for

, então
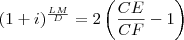
e daí

.
Finalmente,
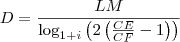
.
Não sei as restrições sobre

, mas devemos ter

e mais algumas condições para existência do logaritmo.
Editado: corrigindo um erro.
Editado pela última vez por
MarceloFantini em Qui Ago 23, 2012 17:12, em um total de 1 vez.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Alce » Qui Ago 23, 2012 16:56
por Alce » Qui Ago 23, 2012 16:56
Muito obrigado Marcelo, me forneceu uma grande ajuda. Confesso que ainda estou com dificuldade para executar a fórmula com a nova formatação em função do algorítimo. Se não fosse pedir muito, teria como me demonstrar a resolução da equação com valores reais? Segue os valores que utilizei no meu trabalho:
LM=180
CE=6
CF=5,36
i=1,5
Na fórmula:
180(6 - 5,36)=5,36(180/2)x(1+1,5)^180/D
Desde já agradeço...
-
Alce
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Ago 23, 2012 14:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Controladoria
- Andamento: formado
 por MarceloFantini » Qui Ago 23, 2012 17:16
por MarceloFantini » Qui Ago 23, 2012 17:16
A propósito, cometi um erro. O resultado final será
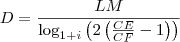
, pois

. Substituindo os valores, teremos:
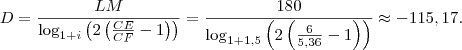
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Isolar Variável] Ajuda para isolar variável na equação
por Gabriel Gomes » Sex Fev 03, 2012 08:55
- 1 Respostas
- 10703 Exibições
- Última mensagem por MarceloFantini

Sáb Fev 04, 2012 12:51
Sistemas de Equações
-
- Isolar variável em Formula.
por viniciusbmello » Sex Jan 23, 2015 16:42
- 5 Respostas
- 4689 Exibições
- Última mensagem por viniciusbmello

Seg Jan 26, 2015 11:29
Equações
-
- [Isolar variável]Conclusão de exercício
por Bellamv » Ter Mai 14, 2013 03:29
- 0 Respostas
- 1327 Exibições
- Última mensagem por Bellamv

Ter Mai 14, 2013 03:29
Álgebra Elementar
-
- Isolar uma variável numa equação de grau 3
por KleinIll » Dom Abr 24, 2016 16:37
- 0 Respostas
- 7160 Exibições
- Última mensagem por KleinIll

Dom Abr 24, 2016 16:37
Equações
-
- Problema para isolar uma variável ---> "L"
por chenz » Sex Out 01, 2021 09:10
- 2 Respostas
- 8321 Exibições
- Última mensagem por chenz

Sáb Out 09, 2021 14:20
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , então
, então 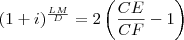
 .
.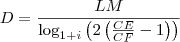 .
. , mas devemos ter
, mas devemos ter  e mais algumas condições para existência do logaritmo.
e mais algumas condições para existência do logaritmo.

 . Substituindo os valores, teremos:
. Substituindo os valores, teremos: