Tah, entendí que um sistema possível e indeterminado é um que apresenta infinitas soluções, pois, tais soluções serão as mesmas que as das equações lineares contidas nele.. só que não tenho idéia de como fazer para chegar a alguma resposta para este problema em específico.
Calcule k tal que
{x=2
{x+2y=8
{3x-2y+kz=0
a)seja um sistema possível e indeterminado;
b)seja um sistema possível e deerminado.
cheguei a y=3, mas não consegui sair disso..


 e
e  , então
, então 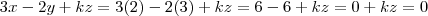 . Isto tem solução para qualquer
. Isto tem solução para qualquer 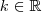 , pois se
, pois se  , é óbvio. Se
, é óbvio. Se  , então
, então  e tem solução novamente.
e tem solução novamente. 

 . Então
. Então 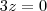 , de onde segue que
, de onde segue que  , então
, então 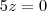 , de onde segue que
, de onde segue que 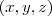 , onde
, onde  .
.  então teremos
então teremos 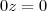 . Como um dos fatores já é zero, isso significa que
. Como um dos fatores já é zero, isso significa que  pode ser qualquer número real. Suponha
pode ser qualquer número real. Suponha  , então
, então 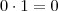 ; suponha agora que
; suponha agora que  . Então
. Então 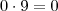 , é solução também. Note que já achamos
, é solução também. Note que já achamos 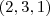 e
e 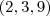 como soluções. Podemos seguir indefinidamente, para qualquer valor real de
como soluções. Podemos seguir indefinidamente, para qualquer valor real de 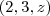 , onde
, onde ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)