 por moyses » Dom Jul 29, 2012 23:35
por moyses » Dom Jul 29, 2012 23:35
Olá pessoal beleza ? Vocês podem me ajudar! como interpretar essa questão?
(PUC-MG) O quadrado da diferença entre o número natural x e 4 e acrescido da soma de x com 8. Então , o resultado é dividido pelo dobro de x, obtendo-se um numero menor do que 2. A soma dos possíveis valores de x é:
A)11
B)22
C)33
D)44
Obs:> Tentei fazer mais a soma da 40 veja só(acho que eu estor fazendo isso errado

)
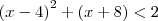
??
-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por e8group » Seg Jul 30, 2012 00:54
por e8group » Seg Jul 30, 2012 00:54
Boa noite , Vamos por partes .
1)
moyses escreveu:quadrado da diferença entre o número natural x e 4 e acrescido da soma de x com 8
Seja ,
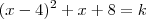
2 )
moyses escreveu:Então , o resultado é dividido pelo dobro de x, obtendo-se um numero menor do que 2
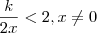
, com isso
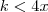
,logo
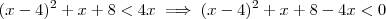
.Portanto ,
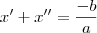
, feito isso acredito que você deve calcular
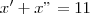
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Seg Jul 30, 2012 01:02
por Russman » Seg Jul 30, 2012 01:02
Como diria Jack, O Estripador, vamos por partes!
moyses escreveu:O quadrado da diferença entre o número natural x e 4
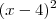
moyses escreveu:e acrescido da soma de x com 8
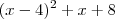
moyses escreveu:Então , o resultado é dividido pelo dobro de x, obtendo-se um numero menor do que 2
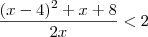
Agora, resolver o problema é solucionar a inequação obtida!
Solução:
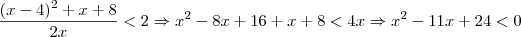
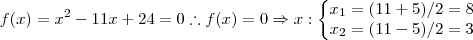
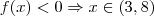
.
Logo, os possíveis valores são

cuja soma é

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por moyses » Seg Jul 30, 2012 09:02
por moyses » Seg Jul 30, 2012 09:02
A minha maior dificuldade foi a de interpretar o texto! Eu achava que era pra resolver primeiro e depois dividir por 2x dando um numero menor que 2! ou eu colocava todo o primeiro membro da equção menor do que 2 direto sem dividar por 2x como você santhiago e Russman fizeram. Parabéns a todos vocês do forum Obrigado há todos vocês!
Mais a soma é 11 ou 22? Por que o santhiago somou os valores das raízes da equação deu 11, e o Russman somou os valores entre as raizes deu 22? Eu acho que a soma é 22! Por que no enunciado pede isso. Mais obrigado desde já pela idéia!

Obs: vocês podem me dar uma dica como interpretar textos de matematica como esse com mais facilidade?
-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por Russman » Seg Jul 30, 2012 09:12
por Russman » Seg Jul 30, 2012 09:12
O enunciado pede claramente a soma de todos os possíveis valores de

. Como este deve ser Natural então o numero de possibilidades é finito dentro de um intervalo.
A dica q eu posso lhe dar para este tipo de problema é a inicial da resolução: vá por partes!
Bons estudos.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por moyses » Ter Jul 31, 2012 16:35
por moyses » Ter Jul 31, 2012 16:35
obrigado! valeww cara!

-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação do 3º grau] Questão da CEFET-PR
por PedroCunha » Dom Set 23, 2012 11:46
- 14 Respostas
- 8851 Exibições
- Última mensagem por PedroCunha

Seg Nov 12, 2012 20:43
Equações
-
- [Equação do Segundo Grau] Questão da Fuvest
por ALPC » Ter Jan 15, 2013 17:25
- 3 Respostas
- 4212 Exibições
- Última mensagem por Cleyson007

Qua Jan 16, 2013 14:12
Equações
-
- Equação do 1º Grau - Como montar a equação
por macedo1967 » Sáb Out 07, 2017 12:53
- 1 Respostas
- 8032 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:17
Equações
-
- [Equação Modular] com equação de 2º grau
por paola-carneiro » Qui Abr 05, 2012 15:53
- 2 Respostas
- 3410 Exibições
- Última mensagem por paola-carneiro

Sex Abr 06, 2012 16:23
Funções
-
- Equação do 1 Grau
por luanxd » Ter Jan 26, 2010 00:06
- 3 Respostas
- 5512 Exibições
- Última mensagem por Cleyson007

Qua Jan 27, 2010 20:40
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 )
)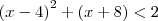 ??
??

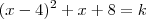
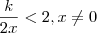 , com isso
, com isso 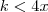 ,logo
,logo 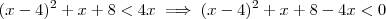 .Portanto ,
.Portanto , 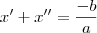 , feito isso acredito que você deve calcular
, feito isso acredito que você deve calcular 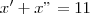

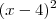
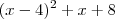
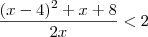
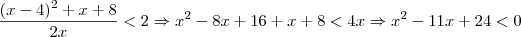
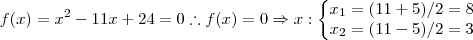
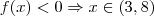 .
. cuja soma é
cuja soma é  .
. . Como este deve ser Natural então o numero de possibilidades é finito dentro de um intervalo.
. Como este deve ser Natural então o numero de possibilidades é finito dentro de um intervalo.

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.