






 e
e 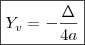

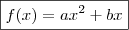

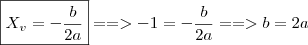

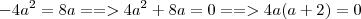
 temos
temos  , com isso,
, com isso, 
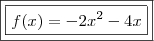

Ricardogferreira escreveu:Infelizmente não consegui anexar a imagem (não permite formato pdf). Os gráficos são gráficos de parábolas. O exercício vem no meu manual.

 tentei resolver o "gráfico B", mas não consegui. O "gráfico C" nem tentei porque o problema que eu tenho é o mesmo, ou seja, como não sei o valor de "c" fico com 3 incógnitas. Explicando o que consegui descobrir do "gráfico B":
tentei resolver o "gráfico B", mas não consegui. O "gráfico C" nem tentei porque o problema que eu tenho é o mesmo, ou seja, como não sei o valor de "c" fico com 3 incógnitas. Explicando o que consegui descobrir do "gráfico B":
Ricardogferreira escreveu:Obrigado Daniel,
Desculpe incomodar novamente. Compreendi a sua explicação, mas fiquei com algumas dúvidas:
Ricardogferreira escreveu:1.ª - Quando você diz que b = - 4 é porque o gráfico corta o eixo y no sentido descendente? É que substituindo o a = - 2 na equação - b^2 = 8a, fica b^2= 16, Logo, b = +4 ou -4
 , a equação será
, a equação será 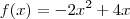 e as raízes
e as raízes  e
e  . Mas, de acordo com o enunciado...
. Mas, de acordo com o enunciado...  e
e 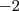 .
.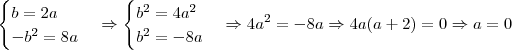 e
e 
 , devemos desconsiderar pois,
, devemos desconsiderar pois,  . Ou seja, se
. Ou seja, se  a função seria de grau 1!
a função seria de grau 1! :
: 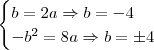
 :
: 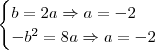 VERDADEIRO
VERDADEIRO :
:  FALSO
FALSO
Ricardogferreira escreveu:...
dados fornecidos no gráfico B (concavidade para cima)- Xv: 2; Yv: 1; GRÁFICO CORTA O EIXO Y EM 3, NO SENTIDO DECRESCENTE - Solução: g(x) = 1/2 (x-2)^2 + 1
...
Ricardo
Ricardogferreira escreveu:...
2.ª - A segunda dúvida é mais gravetentei resolver o "gráfico B", mas não consegui. O "gráfico C" nem tentei porque o problema que eu tenho é o mesmo, ou seja, como não sei o valor de "c" fico com 3 incógnitas. Explicando o que consegui descobrir do "gráfico B":
Logo,
Logo,
Agora não consigo sair daqui. Precisava da sua ajuda de novo, se não for pedir muito.
Obrigado
Ricardo
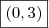

 ==>
==> ![-\left[{(-4a)}^{2} - 12a\right] -\left[{(-4a)}^{2} - 12a\right]](/latexrender/pictures/3eed2897e0df7f2643405466c060295f.png) = 4a ==> - (16
= 4a ==> - (16 - 12a) = 4a ==> -16
- 12a) = 4a ==> -16 + 8a = 0 ==> a(-16a+8) = 0 ==> a= 0 (Falso: porque a > 0) ou a =
+ 8a = 0 ==> a(-16a+8) = 0 ==> a= 0 (Falso: porque a > 0) ou a = 
 ) = - 2
) = - 2 + bx + c
+ bx + c
 - 2x + 3
- 2x + 3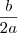 )^2 -
)^2 -  como pretendido nas soluções:
como pretendido nas soluções: (x-2)^2 + 1
(x-2)^2 + 1
 , também conseguiu?
, também conseguiu?

Ricardogferreira escreveu:A outra conclusão é que ainda tenho muito a aprender ...
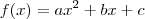 ;
; , onde
, onde  e
e  são as raízes da função;
são as raízes da função;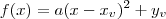 , onde
, onde 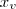 e
e  são as coordenadas do vértice da parábola.
são as coordenadas do vértice da parábola. ,
,  ,
,  e
e  .
.![f(x) = a[x - (-1)]^2 + 2 \implies f(x) = a(x+1)^2 + 2 f(x) = a[x - (-1)]^2 + 2 \implies f(x) = a(x+1)^2 + 2](/latexrender/pictures/128a612332256c5feeea36b6750a6f46.png)


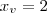 ,
,  , g(0) = 3 (pois o gráfico corta o eixo y em 3).
, g(0) = 3 (pois o gráfico corta o eixo y em 3). ,
,  e h(0) = -2 (pois o gráfico corta o eixo y em -2).
e h(0) = -2 (pois o gráfico corta o eixo y em -2). \implies h(x) = a(x + 1)(x - 3) h(x) = a[x - (-1)](x - 3) \implies h(x) = a(x + 1)(x - 3)](/latexrender/pictures/8f518bc5da51e4fbe62a8e873ccb6bb7.png)
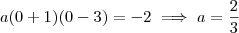
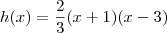
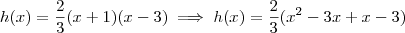
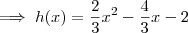
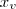 e
e  :
: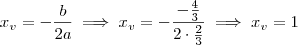
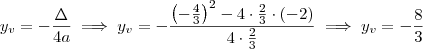
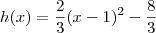

 = 2
= 2 = 1
= 1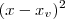 +
+ 
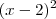 + 1
+ 1 + 1
+ 1  3 = 4a + 1
3 = 4a + 1  a =
a = 

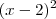 + 1
+ 1
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.