santhiago escreveu:Determine todas a matrizes A,2x2,que comutam com toda matriz B,2x2 ,ou seja tais que AB = BA ,para toda matriz B,2x2 .
Solução (só encontrei uma,o enunciado pede todas ) :
Considerem
![B =\begin{bmatrix} c & g\\ f& d\end{bmatrix} , [B ] _{ij} \in \mathbb{R} B =\begin{bmatrix} c & g\\ f& d\end{bmatrix} , [B ] _{ij} \in \mathbb{R}](/latexrender/pictures/7be512aa027e735b0eeb6c247465521f.png)
e
![A =\begin{bmatrix} x & y\\ z& w\end{bmatrix} , [A]_{ij} \in \mathbb{R} A =\begin{bmatrix} x & y\\ z& w\end{bmatrix} , [A]_{ij} \in \mathbb{R}](/latexrender/pictures/a451a1cc2f9672414664c2340b94309e.png)
de tal forma que
![[AB]_{ij} = [BA]_{ij} [AB]_{ij} = [BA]_{ij}](/latexrender/pictures/7981eb7bfdca055df30dfe7139ebabf2.png)
ou seja ,

.
Então temos que
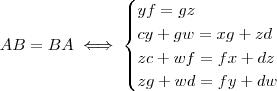 (A parti daí eu não consigo deixar de uma forma explícita cada elemento da matriz A em função dos elementos da matriz B,então criei uma condição que seja verdadeira )
(A parti daí eu não consigo deixar de uma forma explícita cada elemento da matriz A em função dos elementos da matriz B,então criei uma condição que seja verdadeira ) Comparando os elementos
![[AB]_{ij} =[BA]_{ij} [AB]_{ij} =[BA]_{ij}](/latexrender/pictures/f291974712109b820a758c8d6fc5e5b3.png)
para i =1,j=1 em particular para
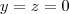
segue que
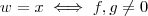
.Ou seja A é uma matriz diagonal onde seus elementos são iguais , desta forma

para toda matriz B ,2x2 .
OBS.:
Esta é uma solução entretanto existe outras por exemplo 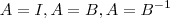
Suponha que B seja dada no problema. O objetivo é descobrir A.
Considerando as matrizes que você colocou, teremos o sistema (revise suas contas):
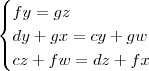
Podemos ainda arrumar esse sistema no formato:
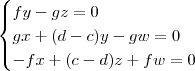
Esse sistema possui infinitas soluções.
Como há mais incógnitas do que equações, vamos ter que escrever algumas incógnitas em função das outras.
Na primeira equação, caso f seja não nulo, obtemos que y = (g/f)z. Substituindo isso na segunda equação, ficamos com:
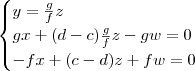
Note que a incógnita y já está em função de z. Além disso, perceba que multiplicando a segunda equação por -f/g (supondo que g não é nulo), obtemos a terceira equação. Disso temos então que
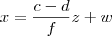
.
Conclusão: dada a matriz
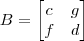
, com f e g não nulos, todas as matrizes que comutam com B possuem o formato
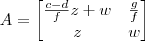
. Note que para cada escolha de z e w obtemos uma matriz diferente. Em outras palavras, dada essa matriz B, podemos encontrar infinitas matrizes A que comutam com essa matriz B.
Agora pense nos casos onde f ou g são nulos.
![B =\begin{bmatrix} c & g\\ f& d\end{bmatrix} , [B ] _{ij} \in \mathbb{R} B =\begin{bmatrix} c & g\\ f& d\end{bmatrix} , [B ] _{ij} \in \mathbb{R}](/latexrender/pictures/7be512aa027e735b0eeb6c247465521f.png) e
e ![A =\begin{bmatrix} x & y\\ z& w\end{bmatrix} , [A]_{ij} \in \mathbb{R} A =\begin{bmatrix} x & y\\ z& w\end{bmatrix} , [A]_{ij} \in \mathbb{R}](/latexrender/pictures/a451a1cc2f9672414664c2340b94309e.png) de tal forma que
de tal forma que ![[AB]_{ij} = [BA]_{ij} [AB]_{ij} = [BA]_{ij}](/latexrender/pictures/7981eb7bfdca055df30dfe7139ebabf2.png) ou seja ,
ou seja ,  .
.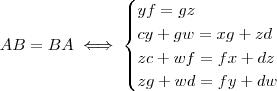
![[AB]_{ij} =[BA]_{ij} [AB]_{ij} =[BA]_{ij}](/latexrender/pictures/f291974712109b820a758c8d6fc5e5b3.png) para i =1,j=1 em particular para
para i =1,j=1 em particular para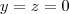 segue que
segue que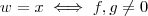 .Ou seja A é uma matriz diagonal onde seus elementos são iguais , desta forma
.Ou seja A é uma matriz diagonal onde seus elementos são iguais , desta forma  para toda matriz B ,2x2 .
para toda matriz B ,2x2 .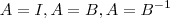


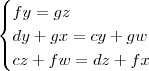
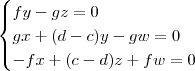

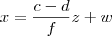 .
.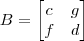 , com f e g não nulos, todas as matrizes que comutam com B possuem o formato
, com f e g não nulos, todas as matrizes que comutam com B possuem o formato 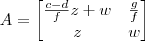 . Note que para cada escolha de z e w obtemos uma matriz diferente. Em outras palavras, dada essa matriz B, podemos encontrar infinitas matrizes A que comutam com essa matriz B.
. Note que para cada escolha de z e w obtemos uma matriz diferente. Em outras palavras, dada essa matriz B, podemos encontrar infinitas matrizes A que comutam com essa matriz B.
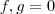 segue que ,
segue que ,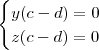 .Supondo
.Supondo 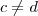 implica
implica 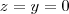 ,sendo assim
,sendo assim  é uma matriz diagonal ,onde
é uma matriz diagonal ,onde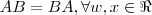 . Agora ,caso
. Agora ,caso 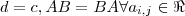 já que
já que será uma matriz com os elementos da diagonal iguais e os demais nulos .
será uma matriz com os elementos da diagonal iguais e os demais nulos .

 , avisa que eu resolvo.
, avisa que eu resolvo.

