 por Rafael16 » Qui Jul 19, 2012 23:10
por Rafael16 » Qui Jul 19, 2012 23:10
Boa noite pessoal,
(FESP-SP) Em um triângulo equilátero de lado L, se unirmos os pontos médios de seus lados obtemos um novo triângulo equilátero. Se procedermos assim sucessivamente obteremos novos triângulos equiláteros, cada vez menores. O limite da soma das áreas dos triângulos equiláteros formados é:
Compreendi isso da seguinte maneira:
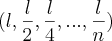
Joguei na fórmula da soma de termos finitos, pois de acordo com o problema, haverá um limite.
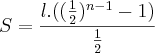
A partir daqui não sei como prosseguir...
Resposta:
![{l}^{2}.\frac{\sqrt[]{3}}{3} {l}^{2}.\frac{\sqrt[]{3}}{3}](/latexrender/pictures/d5d13ef347073d1ab4e7418e395756ad.png)
Valeu pessoal!
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por Arkanus Darondra » Sex Jul 20, 2012 00:37
por Arkanus Darondra » Sex Jul 20, 2012 00:37
Rafael16 escreveu:Joguei na fórmula da soma de termos finitos, pois de acordo com o problema, haverá um limite.
Errado. Temos um P.G.
infinita e decrescente.
Entenda "limite" como valor para o qual tende ou converge a soma.
Além disso você deverá encontrar a razão q entre as
áreas.
Com isso, basta você utilizar a fórmula
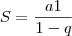
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Sex Jul 20, 2012 02:17
por Russman » Sex Jul 20, 2012 02:17
Eu acredito que a área do n-ésimo triângulo formado se dá por
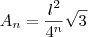
.
Assim, a progressão é
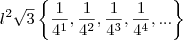
onde
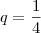
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por e8group » Sex Jul 20, 2012 11:44
por e8group » Sex Jul 20, 2012 11:44
Eu acho que tem como fazer assim também ,
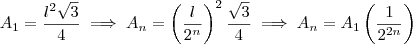
.Visto que

é a área do triângulo equilátero e
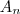
é n-ésima área após

divisões , a parti daí segue que a soma é representado por
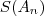
, onde :
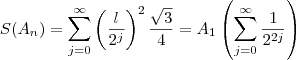
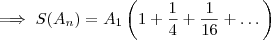
Atribuindo uma variável a
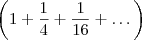
com certeza obterá algo . Vale lembra que pela formula de P.G infinita decrescente obterá a soma cuja razão é

onde ,
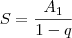
,Lembrando que
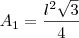
e
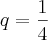
.Com isso você obtém a soma (até mais fácil haha ) ...
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
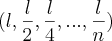
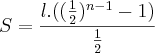
![{l}^{2}.\frac{\sqrt[]{3}}{3} {l}^{2}.\frac{\sqrt[]{3}}{3}](/latexrender/pictures/d5d13ef347073d1ab4e7418e395756ad.png)


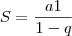
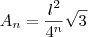 .
.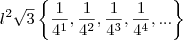
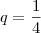 .
.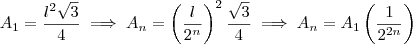 .Visto que
.Visto que  é a área do triângulo equilátero e
é a área do triângulo equilátero e 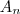 é n-ésima área após
é n-ésima área após  divisões , a parti daí segue que a soma é representado por
divisões , a parti daí segue que a soma é representado por 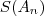 , onde :
, onde :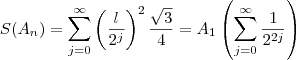
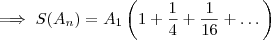
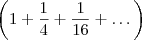 com certeza obterá algo . Vale lembra que pela formula de P.G infinita decrescente obterá a soma cuja razão é
com certeza obterá algo . Vale lembra que pela formula de P.G infinita decrescente obterá a soma cuja razão é  onde ,
onde , 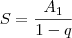 ,Lembrando que
,Lembrando que 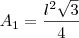 e
e 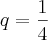 .Com isso você obtém a soma (até mais fácil haha ) ...
.Com isso você obtém a soma (até mais fácil haha ) ...
 .
.



