Sabendo que senx = 1/2 e 0 ? x? ?/2, calcule:
a) cosx
b) cos (x + ?/2)
Bom, se senx é 1/2 e x está no primeiro quadrante, então x só pode ser 30º (penso eu.). Logo cosx = (raiz quadrada de 3)/2
e a alternativa b) cos (x + ?/2) = cosx + cos ?/2 => cos (x + ?/2) =
![\frac{\sqrt[]{3}}{2} \frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png) , pois cos ?/2 é zero. Apenas apliquei a distributiva e resolvi. Também cheguei a pensar
, pois cos ?/2 é zero. Apenas apliquei a distributiva e resolvi. Também cheguei a pensar cos x = sen (90-x), mas não tive sucesso.
O problema é que as respostas que constam no livro são diferentes. para cos (x + ?/2) a resposta é -1/2 e não
![\frac{\sqrt[]{3}}{2} \frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png) . E isso acontece com as outras alternativas, com excessão da letra a) . Onde estou errado? (ou é o livro?) Grato !
. E isso acontece com as outras alternativas, com excessão da letra a) . Onde estou errado? (ou é o livro?) Grato !

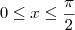 , então teremos
, então teremos 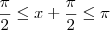 .
. 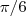 radianos, daí
radianos, daí  .
.

 cos30º + cos 60º
cos30º + cos 60º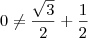
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)