Sabendo que senx = 1/2 e 0 ? x? ?/2, calcule:
a) cosx
b) cos (x + ?/2)
Bom, se senx é 1/2 e x está no primeiro quadrante, então x só pode ser 30º (penso eu.). Logo cosx = (raiz quadrada de 3)/2
e a alternativa b) cos (x + ?/2) = cosx + cos ?/2 => cos (x + ?/2) =
![\frac{\sqrt[]{3}}{2} \frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png) , pois cos ?/2 é zero. Apenas apliquei a distributiva e resolvi. Também cheguei a pensar
, pois cos ?/2 é zero. Apenas apliquei a distributiva e resolvi. Também cheguei a pensar cos x = sen (90-x), mas não tive sucesso.
O problema é que as respostas que constam no livro são diferentes. para cos (x + ?/2) a resposta é -1/2 e não
![\frac{\sqrt[]{3}}{2} \frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png) . E isso acontece com as outras alternativas, com excessão da letra a) . Onde estou errado? (ou é o livro?) Grato !
. E isso acontece com as outras alternativas, com excessão da letra a) . Onde estou errado? (ou é o livro?) Grato !

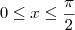 , então teremos
, então teremos 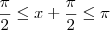 .
. 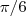 radianos, daí
radianos, daí  .
.

 cos30º + cos 60º
cos30º + cos 60º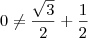
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.