Estou resolvendo uma lista de exercícios e me deparei com esses dois aqui. Eu até desenvolvi mas, a resposta não bate.
1) Calcule
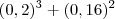= Bom, eu sei que, 
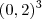é = 0,2 . 0.2 . 0,2 = 0,8 e 
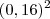= 0,16 . 0,16 = 0,256Só que eu procurei a resposta e não bate
Resposta é 0,0336.
2) (FATEC) Se x e y são números reais tais que x =
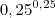e y = 
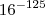, é verdade que:(A) x = y
(B) x > y
(C) x.y =
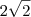
(D) x - y é um número irracional
(E) x + y é um número racional não inteiro
Então, eu fatorei
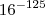e da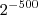 
Se usar notação científica no 
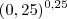da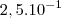 
É isso ai pessoal... Abras
?
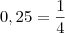
e 0,25 =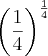 
![0,25^{0,25} = \frac{1}{4}^{\frac{1}{4}} = (4^{-1})^{\frac{1}{4}}=(2^{-2})^{\frac{1}{4}}= 2^{-\frac{1}{2}} = \frac{1}{\sqrt[]{2}}](/latexrender/pictures/4a9d823e5eacbc420b1483e386a5cd28.png "0,25^{0,25} = \frac{1}{4}^{\frac{1}{4}} = (4^{-1})^{\frac{1}{4}}=(2^{-2})^{\frac{1}{4}}= 2^{-\frac{1}{2}} = \frac{1}{\sqrt[]{2}}")
.
.
.
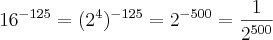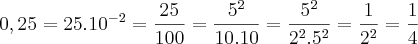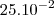Não ter que ser 
1 até 10 ? No caso ficaria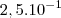 
porque a vírgula se deslocou para a direita? 
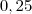para simplificar a expressão . Portanto, não é necessário que o núcleo esteja entre 1 e 10.
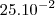como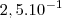 
, pois 
. A difenrença é qe da segunda forma está de acordo com as regras da Notação Científica.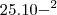
?![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)