Esse exercício eu não consegui resolver mas dei alguns passos:
1) Como AC é diâmetro, então o ângulo B é reto.
2)Aplicando Pitágoras no triângulo ABC temos que AC=
![2\sqrt[2]{5} 2\sqrt[2]{5}](/latexrender/pictures/50db8eb582e7374b38b60d4c3393db8a.png) .
.À partir daí não sei o que fazer. Marquei então o ponto E no qual a bissetriz de B intercepta AC. Percebi que ABD e EBC são semelhantes. No entanto é necessário conhecer mais valores para aplicar a relação de semelhança. Não sei se para continuar o exercício devo usar relações trigonométricas(seno, tangente, etc.) . Tentei lembrar de algo que meu professor ensinou como o Teorema da Bissetriz Interna.
Por favor me ajudem.


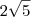 .
. 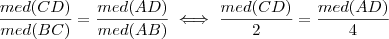
 .
.  .
.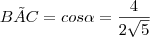 .
.![[med(BD)]^2 = [med(AB)]^2 + [med(AD)]^2 - 2 med(AB) med(AD) . cos \alpha [med(BD)]^2 = [med(AB)]^2 + [med(AD)]^2 - 2 med(AB) med(AD) . cos \alpha](/latexrender/pictures/92f70526da6bd6cfeeebe16d17dcc63f.png) .
.
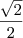 . Logo aplicamos a lei dos cossenos novamente para o lado DE desse triângulo.
. Logo aplicamos a lei dos cossenos novamente para o lado DE desse triângulo. 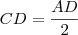
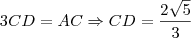
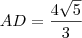
 e que DBC = BBA = 45º
e que DBC = BBA = 45º


 é superior ao diâmetro do círculo que o
é superior ao diâmetro do círculo que o 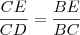 .
.


 .
.



