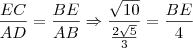por anfran1 » Dom Jul 08, 2012 12:27
por anfran1 » Dom Jul 08, 2012 12:27
13. (OSCM 2009 - Adaptada) Seja ABC um triângulo inscrito em uma circunferência em que o lado AC do triângulo é um diâmetro. A bissetriz de B intercepta a circunferência no ponto D. Sabendo que AB=4 e que BC=2 , calcule BD.
Esse exercício eu não consegui resolver mas dei alguns passos:
1) Como AC é diâmetro, então o ângulo B é reto.
2)Aplicando Pitágoras no triângulo ABC temos que AC=
![2\sqrt[2]{5} 2\sqrt[2]{5}](/latexrender/pictures/50db8eb582e7374b38b60d4c3393db8a.png)
.
À partir daí não sei o que fazer. Marquei então o ponto E no qual a bissetriz de B intercepta AC. Percebi que ABD e EBC são semelhantes. No entanto é necessário conhecer mais valores para aplicar a relação de semelhança. Não sei se para continuar o exercício devo usar relações trigonométricas(seno, tangente, etc.) . Tentei lembrar de algo que meu professor ensinou como o Teorema da Bissetriz Interna.
Por favor me ajudem.
-
anfran1
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jun 28, 2012 18:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Dom Jul 08, 2012 23:47
por fraol » Dom Jul 08, 2012 23:47
Boa noite,
Fiz um desenho auxiliar:

- tria.png (12.26 KiB) Exibido 5398 vezes
Você determinou que AC mede
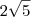
.
O teorema da bissetriz interna trata da relação entre os lados adjacentes ao ângulo e os segmentos, no lado oposto, determinados pela bissetriz. Isto é:
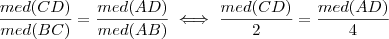

.
Então

.
Por outro lado, o cosseno do ângulo
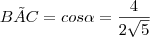
.
Com estes dados você pode aplicar a lei dos cossenos (você a conhece?) e assim obter a medida de BD:
![[med(BD)]^2 = [med(AB)]^2 + [med(AD)]^2 - 2 med(AB) med(AD) . cos \alpha [med(BD)]^2 = [med(AB)]^2 + [med(AD)]^2 - 2 med(AB) med(AD) . cos \alpha](/latexrender/pictures/92f70526da6bd6cfeeebe16d17dcc63f.png)
.
Basta substituir os valores.
Se achar alguma passagem obscura manda de volta pra gente discutir.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Arkanus Darondra » Seg Jul 09, 2012 00:09
por Arkanus Darondra » Seg Jul 09, 2012 00:09
fraol escreveu:Se achar alguma passagem obscura manda de volta pra gente discutir.
Não analisei toda a resolução, porém, observando a figura, creio que a localização do ponto D esteja errada.
O ponto deveria estar sobre a circunferência, no ponto de intersecção com a bissetriz do ângulo reto.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Seg Jul 09, 2012 02:28
por fraol » Seg Jul 09, 2012 02:28
Arkanus Darondra escreveu:fraol escreveu:Se achar alguma passagem obscura manda de volta pra gente discutir.
Não analisei toda a resolução, porém, observando a figura, creio que a localização do ponto D esteja errada.
O ponto deveria estar sobre a circunferência, no ponto de intersecção com a bissetriz do ângulo reto.
Tem razão. Não atentei ao enunciado quanto a posição do ponto D.
Bom, para não refazer o desenho vamos chamar o tal ponto de interseção da bissetriz de E.
Por propriedades da bissetriz concluiremos que AE e CE são iguais e portanto que os ângulos DÂE e DCE são iguais e valem 45 graus pois AEC vale 90 graus e o triângulo AEC é isósceles. Para calcular AE usamos Pitágoras. AD já temos da (meia) solução anterior. Então, temos dois lados e o ângulo entre eles. Isto é no triângulo AED sabemos AD, AE e o ângulo cujo cosseno é
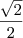
. Logo aplicamos a lei dos cossenos novamente para o lado DE desse triângulo.
Como já temos BD, basta somar com DE para obtermos a resposta final, aí o jeito é fazer as contas .
Arkanus Darondra dá uma geral, por favor, pra ver se não passou mais nada.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Arkanus Darondra » Seg Jul 09, 2012 11:42
por Arkanus Darondra » Seg Jul 09, 2012 11:42
Fraol, como eu desconheço a propriedade da bissetriz que você utilizou, creio que apenas o cálculo de AD esteja errado.
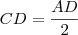
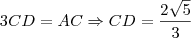
Então
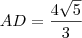
Considerando o Triângulo BEC, temos que BÊC = BÂC =

e que DBC = BBA = 45º
Aplicando a lei dos senos no Triângulo BEC, vem:

Como o Triângulo BEC é semelhante ao Triângulo BAD (caso AA), vem:


Editado pela última vez por
Arkanus Darondra em Ter Jul 10, 2012 14:19, em um total de 1 vez.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por anfran1 » Ter Jul 10, 2012 13:48
por anfran1 » Ter Jul 10, 2012 13:48
Fiquei um pouco confuso com essas marcações. No caso o ponto E que vocês falam seria o ponto D do enunciado e o ponto D que vocês falam seria a ponto E que eu marquei ao tentar resolver o exercício?
E o objetivo é calcular o valor do segmento que vai do vértice B até o ponto da interseção(não sei se o português está correto) entre a bissetriz de B e a circunferência.
E sim, eu conheço a lei dos cossenos.
Desde já eu agradeço.
-
anfran1
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jun 28, 2012 18:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Ter Jul 10, 2012 14:00
por fraol » Ter Jul 10, 2012 14:00
Boa tarde,
anfran1,
Considere E na nossa discussão como sendo o seu ponto D, assim a resposta que se procura é a medida do segmento BE. ( no enunciado que você postou seria BD - desculpe foi confusão minha ).
Arkanus Darondra,
Essa medida

é superior ao diâmetro do círculo que o
anfran1 encontrou.
Obs: Há uma outra relação que, me parece, torna a solução do problema mais simples:
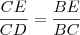
.
Essa relação utiliza alguns resultados que discutimos acima.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por anfran1 » Ter Jul 10, 2012 14:04
por anfran1 » Ter Jul 10, 2012 14:04
fraol escreveu:Boa tarde,
anfran1,
Considere E na nossa discussão como sendo o seu ponto D, assim a resposta que se procura é a medida do segmento BE. ( no enunciado que você postou seria BD - desculpe foi confusão minha ).
Arkanus Darondra,
Essa medida

é superior ao diâmetro do círculo que o
anfran1 encontrou.
Obs: Há uma outra relação que, me parece, torna a solução do problema mais simples:
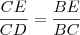
.
Essa relação utiliza alguns resultados que discutimos acima.
.
Obrigado. Só tenho mais uma dúvida. Eu tive de adaptar o exercício por conta própria para que pudesse ser entendido poia havia uma imagem no mesmo. Como faço para postar um imagem?
-
anfran1
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jun 28, 2012 18:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Ter Jul 10, 2012 14:13
por fraol » Ter Jul 10, 2012 14:13
Oi,
Quando você está editando a postagem na parte inferior da caixa de digitação há uma aba com um link "Adicionar um anexo". Ali você pode escolher uma figura armazenada no seu computador e enviar - é necessário dar um nome para a figura, por exemplo: fig1 ou o que você achar conveniente.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Arkanus Darondra » Ter Jul 10, 2012 14:20
por Arkanus Darondra » Ter Jul 10, 2012 14:20
fraol escreveu:Essa medida

é superior ao diâmetro do círculo que o
anfran1 encontrou.
Tem razão. Creio que o erro esteja neste passo:
Arkanus Darondra escreveu: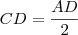

O correto seria 3
CD=AC.
Editei acima.
Obrigado por notar.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por anfran1 » Ter Jul 10, 2012 14:21
por anfran1 » Ter Jul 10, 2012 14:21
Arkanus Darondra escreveu:Fraol, como eu desconheço a propriedade da bissetriz que você utilizou, creio que apenas o cálculo de AD esteja errado.
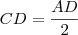

Considerando o Triângulo BEC, temos que BÊC = BÂC =

e que DBC = BBA = 45º
Aplicando a lei dos senos no Triângulo BEC, vem:

Como o Triângulo BEC é semelhante ao Triângulo BAD (caso AA), vem:
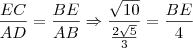

Andei pesquisando em minhas apostilas e achei o tópico que fala sobre o teorema da bissetriz interna.
Aproveitando o desenho acima esse teorema pode ser comprovado da seguinte maneira:
1) Traça-se uma parelela (y) à bissetriz BD passando pelo ponto C.
2) Prolonga-se o lado AB até que esse encontre y no ponto K.}
3)Perceba que o triângulo BCK é isósceles, pois os ângulos ABD, DBC, BCK e BKC são todos do mesmo tamanho, portantoos lados BC=BK.
4) Basta aplicar o Teorema de Tales para comprovar a relação.
Isso fica apenas a cargo de curiosidade.
-
anfran1
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jun 28, 2012 18:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Triângulo inscrito
 por laisv11 » Qui Mai 28, 2009 16:33
por laisv11 » Qui Mai 28, 2009 16:33
- 4 Respostas
- 10645 Exibições
- Última mensagem por Molina

Sáb Mai 30, 2009 22:05
Geometria Plana
-
- Triângulo Inscrito
por Fogodc » Seg Abr 05, 2010 23:33
- 0 Respostas
- 1583 Exibições
- Última mensagem por Fogodc

Seg Abr 05, 2010 23:33
Geometria Plana
-
- Triângulo / Inscrito
por Marcelo C Delgado » Qua Nov 10, 2010 16:06
- 3 Respostas
- 2577 Exibições
- Última mensagem por Rogerio Murcila

Qui Nov 18, 2010 19:04
Trigonometria
-
- triangulo inscrito
 por alfabeta » Qui Mar 01, 2012 15:51
por alfabeta » Qui Mar 01, 2012 15:51
- 7 Respostas
- 3672 Exibições
- Última mensagem por MarceloFantini

Dom Mar 04, 2012 20:02
Geometria Plana
-
- triangulo inscrito e circunscrito
por Katia Silveira » Sex Mai 16, 2014 17:46
- 1 Respostas
- 1932 Exibições
- Última mensagem por e8group

Sex Mai 16, 2014 18:07
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![2\sqrt[2]{5} 2\sqrt[2]{5}](/latexrender/pictures/50db8eb582e7374b38b60d4c3393db8a.png) .
.

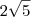 .
. 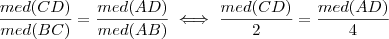
 .
.  .
.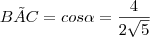 .
.![[med(BD)]^2 = [med(AB)]^2 + [med(AD)]^2 - 2 med(AB) med(AD) . cos \alpha [med(BD)]^2 = [med(AB)]^2 + [med(AD)]^2 - 2 med(AB) med(AD) . cos \alpha](/latexrender/pictures/92f70526da6bd6cfeeebe16d17dcc63f.png) .
.
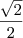 . Logo aplicamos a lei dos cossenos novamente para o lado DE desse triângulo.
. Logo aplicamos a lei dos cossenos novamente para o lado DE desse triângulo. 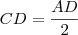
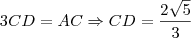
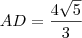
 e que DBC = BBA = 45º
e que DBC = BBA = 45º


 é superior ao diâmetro do círculo que o
é superior ao diâmetro do círculo que o 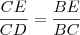 .
.