 por andersoneng » Qua Jun 27, 2012 12:26
por andersoneng » Qua Jun 27, 2012 12:26
Ola Pessoal ! Tenho uma duvida sobre este exercicio --2) Um automóvel que viaja à razão de
30 m/s, aproxima-se de um cruzamento. Quando o automóvelestá a 120 m do cruzamento, um caminhão que viaja à razão de 40 m/s
atravessa o cruzamento. Oautomóvel e o caminhão estão em rodovias que formam um ângulo reto uma com a outra. Com quevelocidade afastam-se o automóvel e o caminhão 2s depois do caminhão passar pelo cruzamento?
duvida-- eu chego na resposta certa do exercicio se eu usar o teorema de pitagoras nas duas equacoes horarias dos espacos.
sa=120-30t e sc 40t, encontrar um novo espaco, derivar este espaco, encontrando assim uma equacao da velocidade e aplicar o t=2s.
mas pq a velocidade do automovel tem de se negativa ::: nao entendo...alguem poderia resolve- la ::
-
andersoneng
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Jun 25, 2012 20:46
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Graduação Engenharia de Produção
- Andamento: cursando
 por e8group » Qua Jun 27, 2012 16:49
por e8group » Qua Jun 27, 2012 16:49
andersoneng escreveu:Ola Pessoal ! Tenho uma duvida sobre este exercicio --2) Um automóvel que viaja à razão de
30 m/s, aproxima-se de um cruzamento. Quando o automóvelestá a 120 m do cruzamento, um caminhão que viaja à razão de 40 m/s
atravessa o cruzamento. Oautomóvel e o caminhão estão em rodovias que formam um ângulo reto uma com a outra. Com quevelocidade afastam-se o automóvel e o caminhão 2s depois do caminhão passar pelo cruzamento?
duvida-- eu chego na resposta certa do exercicio se eu usar o teorema de pitagoras nas duas equacoes horarias dos espacos.
sa=120-30t e sc 40t, encontrar um novo espaco, derivar este espaco, encontrando assim uma equacao da velocidade e aplicar o t=2s.
mas pq a velocidade do automovel tem de se negativa ::: nao entendo...alguem poderia resolve- la ::
Considere a figura abaixo :
Pela figura temos :
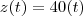
,distância de C em sentido ao cruzamento .

,distância de B em sentido ao cruzamento .

,distância de (B,C) .
logo :

.
Tente resolver agora !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Qua Jun 27, 2012 18:51
por Russman » Qua Jun 27, 2012 18:51
As velocidades tem de ser negativas pois os móveis se APROXIMAM da origem! Lembre-se qe a velocidade é a taxa de variação da posição em relação ao tempo. A medida que o tempo passa as posições vão diminuindo, pois aproximan-se do 0. Assim, a velocidade tem de ser negativa para equacionar realisticamente o problema.
Editado pela última vez por
Russman em Qua Jun 27, 2012 19:20, em um total de 1 vez.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Qua Jun 27, 2012 19:18
por Russman » Qua Jun 27, 2012 19:18
Vou chamar o móvel que viaja na vertical de

e na horizontal de

.
andersoneng escreveu:Quando o automóvelestá a 120 m do cruzamento, um caminhão que viaja à razão de 40 m/s
atravessa o cruzamento.
Assim, em

temos
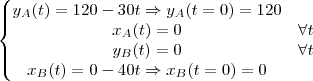
Agora, você tem de calcular a distância entre os móveis a todo instante

a aprtir disso para então derivá-la e obter a velocidade relativa!
Seja
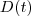
essa distância. Assim,
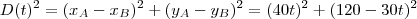
.
Portanto,
![\frac{d}{dt}D(t)^{2} =2D(t)\frac{d}{dt}D(t)=\frac{d}{dt}[ (40t)^{2} + (120-30t)^{2}]\Rightarrow \frac{d}{dt}D(t)^{2} =2D(t)\frac{d}{dt}D(t)=\frac{d}{dt}[ (40t)^{2} + (120-30t)^{2}]\Rightarrow](/latexrender/pictures/bb68abf43ee205618f6dfe6b97d6678d.png)
![\Rightarrow \frac{d}{dt}D(t)=\frac{1}{2D(t)}[2.40t.40-2.(120-30t).30]=\frac{100}{D(t)}(25t-36 ) \Rightarrow \frac{d}{dt}D(t)=\frac{1}{2D(t)}[2.40t.40-2.(120-30t).30]=\frac{100}{D(t)}(25t-36 )](/latexrender/pictures/50101779dafa6643e2399602f26870e7.png)
.
Agora, faça

.
Editado pela última vez por
Russman em Qua Jun 27, 2012 19:31, em um total de 1 vez.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Qua Jun 27, 2012 19:26
por Russman » Qua Jun 27, 2012 19:26
Eu acredito que você deva calcular

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Qua Jun 27, 2012 19:49
por Russman » Qua Jun 27, 2012 19:49
Interessante nesta questão que, a longo prazo, a velocidade de afastamento dos móveis é constante, e igual a 50 m/s! Isto é,

.
(:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por e8group » Qua Jun 27, 2012 21:36
por e8group » Qua Jun 27, 2012 21:36
ooops!
z(t) = 120 - 30(t) .além do mais sua dúvida nem estar relacionada a resolução do exercício e sim uma explicação física p/ as velocidades ser negativas (como nosso amigo explicou acima) , desculpe pelo erro . Abraços !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por andersoneng » Qui Jun 28, 2012 10:24
por andersoneng » Qui Jun 28, 2012 10:24
muito obrigado pelas explicacoes !
abra;os amigos !
-
andersoneng
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Jun 25, 2012 20:46
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Graduação Engenharia de Produção
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Otimizacao
por Taisa » Sex Nov 12, 2010 13:53
- 1 Respostas
- 2140 Exibições
- Última mensagem por MarceloFantini

Sex Nov 12, 2010 14:36
Cálculo: Limites, Derivadas e Integrais
-
- Otimização
 por AlbertoAM » Sáb Mai 14, 2011 21:36
por AlbertoAM » Sáb Mai 14, 2011 21:36
- 4 Respostas
- 2476 Exibições
- Última mensagem por AlbertoAM

Dom Mai 15, 2011 19:23
Cálculo: Limites, Derivadas e Integrais
-
- Otimização
por elbert005 » Ter Mai 31, 2011 15:41
- 4 Respostas
- 3614 Exibições
- Última mensagem por LuizAquino

Ter Mai 31, 2011 18:08
Cálculo: Limites, Derivadas e Integrais
-
- Otimização
por Jhonata » Seg Fev 25, 2013 19:24
- 1 Respostas
- 1403 Exibições
- Última mensagem por Russman

Seg Fev 25, 2013 20:28
Cálculo: Limites, Derivadas e Integrais
-
- oTIMIZAÇÃO
por Pinheiro Rosa Victor » Qui Mai 02, 2013 11:11
- 0 Respostas
- 1248 Exibições
- Última mensagem por Pinheiro Rosa Victor

Qui Mai 02, 2013 11:11
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


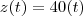 ,distância de C em sentido ao cruzamento .
,distância de C em sentido ao cruzamento . ,distância de B em sentido ao cruzamento .
,distância de B em sentido ao cruzamento . ,distância de (B,C) .
,distância de (B,C) .  .
.
 e na horizontal de
e na horizontal de  .
. temos
temos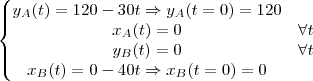
 a aprtir disso para então derivá-la e obter a velocidade relativa!
a aprtir disso para então derivá-la e obter a velocidade relativa!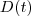 essa distância. Assim,
essa distância. Assim,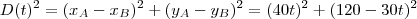 .
.![\frac{d}{dt}D(t)^{2} =2D(t)\frac{d}{dt}D(t)=\frac{d}{dt}[ (40t)^{2} + (120-30t)^{2}]\Rightarrow \frac{d}{dt}D(t)^{2} =2D(t)\frac{d}{dt}D(t)=\frac{d}{dt}[ (40t)^{2} + (120-30t)^{2}]\Rightarrow](/latexrender/pictures/bb68abf43ee205618f6dfe6b97d6678d.png)
![\Rightarrow \frac{d}{dt}D(t)=\frac{1}{2D(t)}[2.40t.40-2.(120-30t).30]=\frac{100}{D(t)}(25t-36 ) \Rightarrow \frac{d}{dt}D(t)=\frac{1}{2D(t)}[2.40t.40-2.(120-30t).30]=\frac{100}{D(t)}(25t-36 )](/latexrender/pictures/50101779dafa6643e2399602f26870e7.png) .
. .
. .
. .
. em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.