 por jann lucca » Sex Jun 15, 2012 19:41
por jann lucca » Sex Jun 15, 2012 19:41
(ESA-85) Uma loja vendeu 2/5 de um peça de tecido e depois vendeu 5/12 do restante. O que sobrou foi vendido por r$1400,00. Sabendo-se que o tecido foi vendido a R$5,00o metro, o comprimento inicial da peça era de:
a)200m
b)400m
c)800m
d)1200m
e)1600m
-
jann lucca
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Mai 11, 2012 17:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Educação Física
- Andamento: cursando
 por Russman » Sex Jun 15, 2012 20:57
por Russman » Sex Jun 15, 2012 20:57
jann lucca escreveu:(ESA-85) Uma loja vendeu 2/5 de um peça de tecido e depois vendeu 5/12 do restante. O que sobrou foi vendido por r$1400,00. Sabendo-se que o tecido foi vendido a R$5,00o metro, o comprimento inicial da peça era de:
a)200m
b)400m
c)800m
d)1200m
e)1600m
Faça o preço do comprimento inicial da peça ser

. Assim,
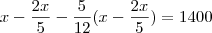
.
Você entende como chegar nessa equação?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por DanielFerreira » Sex Jun 15, 2012 21:03
por DanielFerreira » Sex Jun 15, 2012 21:03
jann lucca escreveu:(ESA-85) Uma loja vendeu 2/5 de um peça de tecido e depois vendeu 5/12 do restante. O que sobrou foi vendido por r$1400,00. Sabendo-se que o tecido foi vendido a R$5,00o metro, o comprimento inicial da peça era de:
a)200m
b)400m
c)800m
d)1200m
e)1600m
Acho que há algo de errado com o enunciado!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por jann lucca » Sex Jun 15, 2012 22:34
por jann lucca » Sex Jun 15, 2012 22:34
Valeu, Russman! Deu certo aqui! A resposta foi 800m. A equação que eu tava fazendo aqui tava mais ou menos parecida com essa...Agora está claro. Entendi.
-
jann lucca
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Mai 11, 2012 17:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Educação Física
- Andamento: cursando
 por DanielFerreira » Sex Jun 15, 2012 23:27
por DanielFerreira » Sex Jun 15, 2012 23:27
Jann Lucca,
desenvolvendo a equação encontrada pelo Russman, teremos x = 4.000
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Russman » Sex Jun 15, 2012 23:40
por Russman » Sex Jun 15, 2012 23:40
Siiim, x= 4000 reais.
Para saber o comprimento basta dividir 4000 reais por 5 reais/metro! Isso calcula 800 m. (:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por DanielFerreira » Sex Jun 15, 2012 23:58
por DanielFerreira » Sex Jun 15, 2012 23:58
Russman escreveu:Siiim, x= 4000 reais.
Para saber o comprimento basta dividir 4000 reais por 5 reais/metro! Isso calcula 800 m. (:
Vlw Russman pelo esclarecimento, interpretei erradamente o enunciado.
Me desculpem!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por jvictorsst » Qui Mar 17, 2016 13:57
por jvictorsst » Qui Mar 17, 2016 13:57
Alguém desenvolver essa equação não to conseguindo fazer
-
jvictorsst
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Mar 17, 2016 13:53
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- duvidas pra resolver esses exercicios
por simoneribeiro » Qui Set 20, 2012 16:24
- 1 Respostas
- 1731 Exibições
- Última mensagem por MarceloFantini

Qui Set 20, 2012 21:14
Análise Combinatória
-
- [Limite] como resolver esses limites
por Isadora Souza » Seg Jan 07, 2013 15:20
- 1 Respostas
- 1950 Exibições
- Última mensagem por joaofonseca

Seg Jan 07, 2013 19:00
Cálculo: Limites, Derivadas e Integrais
-
- [ESCALONAMENTO] como resolver esses sistemas
 por mayconlucas » Seg Nov 09, 2015 09:39
por mayconlucas » Seg Nov 09, 2015 09:39
- 2 Respostas
- 3546 Exibições
- Última mensagem por nakagumahissao

Ter Nov 10, 2015 15:31
Álgebra Linear
-
- me ajudem calculos para antecipar parcelas
por MABafi » Dom Jul 18, 2010 23:36
- 0 Respostas
- 1605 Exibições
- Última mensagem por MABafi

Dom Jul 18, 2010 23:36
Matemática Financeira
-
- calculos para funçoes de varias variaveis
por flavio970 » Sex Out 16, 2015 22:25
- 0 Respostas
- 3494 Exibições
- Última mensagem por flavio970

Sex Out 16, 2015 22:25
Cálculo para Funções de Várias Variáveis II
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 . Assim,
. Assim,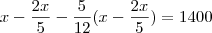 .
.
