- Olá pessoal! Novamente venho recorrer a vocês a fim de sanar minhas dúvidas - agora, sobre geometria anaítica. Bem, estou resolvendo minha antiga apostila do ensino médio sobre Analítica e heis que deparo-me com um problema que parece sem solução.
- O anunciado apresenta uma situação em que dentro de um plano cartesiano possúo apenas três pontos conhecidos de um paralelogramo, devo então encontrar o quarto ponto desta figura. O enunciado também faz a seguinte observação: "As diagonais de um paralelogramo 'encontram-se' em seus respectivos pontos médios".
Pontos do plano: A(0,1), B(2,5), C(3,4) e por dedução, D(X,Y).
Tentativas:
- Tentei usar a definição do paralelogramo - "Um paralelogramo é um polígono de quatro lados (quadrilátero) cujos lados opostos são 'iguais' e 'paralelos'." - para lidar com eqüidistâncias comparando a distância BC com a distância DA, porem de nada adianta porque o resultado em um é inteiro e em outro são duas equações de segundo grau - uma para 'x' e outra para 'y'. Eu precisaria de dois pontos que eqüdistam do ponto 'P' para lidar com a eqüdistância, que foi a unica solução que me veio a cabeça até o momento, porém não existem dois pontos equidistantes de 'P' neste problema. Então fiquei travado nesta.
PS: Pela definição de paralelogramo eu - visualmente - sei que, provavelmente, o ponto 'D' trata-se na verdade de D(1,0) para que BC fique paralelo a AD. Porém não consigo chegar a isto.
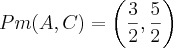
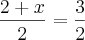
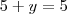
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.