 por FernandaBS » Sex Mai 25, 2012 18:04
por FernandaBS » Sex Mai 25, 2012 18:04
Dada uma função f(x) = arc tg 1/x quando x--> 0, determinar os limites à direita e à esquerda. Não sei como fazer essa questão, alguém pode me ajudar ??
-
FernandaBS
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Mai 25, 2012 10:22
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Guill » Sex Mai 25, 2012 20:16
por Guill » Sex Mai 25, 2012 20:16
Isso deve ser feito analizando o ciclo trigonométrico. Dado o limite:

Podemos convertê-lo para:
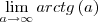
-----> Para valores à direita de x = 0

-----> Para valores à esquerda de x = 0
Sabendo que
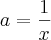
. Essas determinações surgiram da análize da função g(x) =
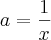
.
Agora fica simples pois, uma vez que sabemos que a tangente tende ao infinito no arco

e tende ao -infinito no arco
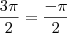
, temos que:

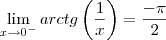
Editado pela última vez por
Guill em Sáb Mai 26, 2012 15:30, em um total de 3 vezes.
-

Guill
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Dom Jul 03, 2011 17:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por FernandaBS » Sex Mai 25, 2012 20:59
por FernandaBS » Sex Mai 25, 2012 20:59
Obrigada Guill.. Mas no gabarito do livro (Diva Flemming) dá

e

..
-
FernandaBS
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Mai 25, 2012 10:22
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Guill » Sáb Mai 26, 2012 15:26
por Guill » Sáb Mai 26, 2012 15:26
FernandaBS escreveu:Obrigada Guill.. Mas no gabarito do livro (Diva Flemming) dá e ..
De fato, é a mesma coisa:

Vou modificar os valores. Eu cometi um pequeno erro de digitação.
-

Guill
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Dom Jul 03, 2011 17:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2787 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
-
- LIMITES LATERAIS
por Fabio Cabral » Qua Out 06, 2010 11:48
- 6 Respostas
- 4237 Exibições
- Última mensagem por Fabio Cabral

Qui Out 07, 2010 11:04
Funções
-
- Limites laterais
por valeuleo » Sáb Abr 09, 2011 21:07
- 8 Respostas
- 5871 Exibições
- Última mensagem por MarceloFantini

Dom Abr 10, 2011 21:00
Cálculo: Limites, Derivadas e Integrais
-
- [Limites laterais] Questão
por Leti Moura » Qui Jun 14, 2012 00:52
- 11 Respostas
- 6563 Exibições
- Última mensagem por Leti Moura

Sáb Jun 16, 2012 21:36
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] Limites laterais..!
por mih123 » Ter Ago 28, 2012 15:40
- 8 Respostas
- 5088 Exibições
- Última mensagem por MarceloFantini

Qua Ago 29, 2012 16:59
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




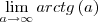 -----> Para valores à direita de x = 0
-----> Para valores à direita de x = 0 -----> Para valores à esquerda de x = 0
-----> Para valores à esquerda de x = 0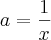 . Essas determinações surgiram da análize da função g(x) =
. Essas determinações surgiram da análize da função g(x) = 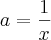 .
.  e tende ao -infinito no arco
e tende ao -infinito no arco 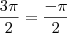 , temos que:
, temos que:
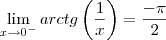

 e
e  ..
..


