



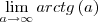 -----> Para valores à direita de x = 0
-----> Para valores à direita de x = 0 -----> Para valores à esquerda de x = 0
-----> Para valores à esquerda de x = 0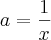 . Essas determinações surgiram da análize da função g(x) =
. Essas determinações surgiram da análize da função g(x) = 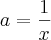 .
.  e tende ao -infinito no arco
e tende ao -infinito no arco 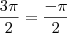 , temos que:
, temos que:
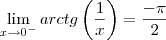

 e
e  ..
..
FernandaBS escreveu:Obrigada Guill.. Mas no gabarito do livro (Diva Flemming) dá e ..


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes

 .
.
 :
: