Estou em dúvida na seguinte questão de otimização: "Prove que entre todos os retângulos com um dado perímetro P, o quadrado é o que possui maior área"
Até onde cheguei:
 e
e 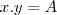 , daí isolo x na primeira equação fica:
, daí isolo x na primeira equação fica: 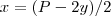 , e levo para A, resultando em
, e levo para A, resultando em  , e aí não sei mais...
, e aí não sei mais...E agora?
abraços!!!




 chego à seguinte expressão:
chego à seguinte expressão:  , dái então eu quero achar o ponto crítico, que resulta em
, dái então eu quero achar o ponto crítico, que resulta em 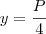 , e agora fico meio confuso...
, e agora fico meio confuso...
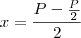

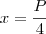
![A=x.y...y=\sqrt[]{{d}^{2}-{x}^{2}} A=x.y...y=\sqrt[]{{d}^{2}-{x}^{2}}](/latexrender/pictures/1c6753e201da7044dc136c1bb0a14656.png) ...logo:
...logo:![A(x)=x.(\sqrt[]{{{d}^{2}-{{x}^{2}}}^{}}) A(x)=x.(\sqrt[]{{{d}^{2}-{{x}^{2}}}^{}})](/latexrender/pictures/e59055c0794be2f953fa1937fa2f5501.png) ...
...![A'(x)=-2x(\sqrt[]{{{d}^{2}-{{x}^{2}}}^{}})+(-2{x}^{3}/(\sqrt[]{{{d}^{2}-{{x}^{2}}}^{}})=0... A'(x)=-2x(\sqrt[]{{{d}^{2}-{{x}^{2}}}^{}})+(-2{x}^{3}/(\sqrt[]{{{d}^{2}-{{x}^{2}}}^{}})=0...](/latexrender/pictures/ffdc5616ffea0a458742c42591d08337.png)
![2x.(d}^{2}-{x}^{2}-{x}^{2}/(\sqrt[]{{{d}^{2}-{{x}^{2}}}^{}}))=0\Rightarrow
x=\sqrt[]{{{d}^{2}-{{x}^{2}}}^{}}=y...x=y... 2x.(d}^{2}-{x}^{2}-{x}^{2}/(\sqrt[]{{{d}^{2}-{{x}^{2}}}^{}}))=0\Rightarrow
x=\sqrt[]{{{d}^{2}-{{x}^{2}}}^{}}=y...x=y...](/latexrender/pictures/c95960edf02a9e515f19b1c9acf794bd.png)

![A'(x)=\sqrt[]{{d}^{2}-{x}^{2}}-2{x}^{2}/(\sqrt[]{{d}^{2}-{x}^{2}}) A'(x)=\sqrt[]{{d}^{2}-{x}^{2}}-2{x}^{2}/(\sqrt[]{{d}^{2}-{x}^{2}})](/latexrender/pictures/e49f37d39305de57320d6862b14c97ee.png)
![A'(x)=({d}^{2}-{x}^{2}-{x}^{2})/(\sqrt[]{{d}^{2}-{x}^{2}})=0...
x=y... A'(x)=({d}^{2}-{x}^{2}-{x}^{2})/(\sqrt[]{{d}^{2}-{x}^{2}})=0...
x=y...](/latexrender/pictures/a70a0c6303c87ca015a1330b02f267a7.png) ...obrigado
...obrigado
 .
.



