por iceman » Qui Mai 10, 2012 18:46
Olá galera, sou novo aqui no fórum e ficaria muito agradecido se pudessem me ajudar em algumas questões, aí vai a primeira:
Determine "k" de modo que o número complexo
Seja imaginário puro.
-
iceman
- Usuário Parceiro
-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
por fraol » Qui Mai 10, 2012 19:28
Boa noite,
Para que o número complexo
seja imaginário puro é necessário que ele não possua a parte real. Então a parte real desse número deve ser igual a 0.
Qual é parte real do número complexo acima?
Iguale essa parte a 0 e resolva a equação para obter a resposta.
.
-
fraol
- Colaborador Voluntário
-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
por iceman » Qui Mai 10, 2012 19:32
fraol escreveu:Boa noite,
Para que o número complexo
seja imaginário puro é necessário que ele não possua a parte real. Então a parte real desse número deve ser igual a 0.
Qual é parte real do número complexo acima?
Iguale essa parte a 0 e resolva a equação para obter a resposta.
.
Amigo, o problema é que eu não sei como que é que faz D; Você poderia montar o cálculo para mim ? Obrigado pela atenção!
-
iceman
- Usuário Parceiro
-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
por fraol » Qui Mai 10, 2012 19:41
Qual é parte real do número complexo acima?
Iguale essa parte a 0 e resolva a equação para obter a resposta.
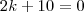
Veja que agora você tem uma equação do primeiro grau. Tente resolvê-la.
.
-
fraol
- Colaborador Voluntário
-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão - números complexos
por Danilo » Sex Ago 03, 2012 02:27
- 1 Respostas
- 2062 Exibições
- Última mensagem por e8group
Sex Ago 03, 2012 11:15
Números Complexos
-
- Questão - Números Complexos
por Glauber_Garcia » Qua Nov 28, 2012 21:25
- 2 Respostas
- 4784 Exibições
- Última mensagem por Direito
Qua Mar 13, 2013 01:15
Números Complexos
-
- [números complexos] questão unicentro
por Flavia R » Qui Ago 25, 2011 11:39
- 4 Respostas
- 3562 Exibições
- Última mensagem por Flavia R
Qui Ago 25, 2011 21:23
Números Complexos
-
- Números complexos - Questão chata
por iceman » Dom Mai 27, 2012 18:08
- 13 Respostas
- 7509 Exibições
- Última mensagem por DanielFerreira
Dom Mai 27, 2012 21:26
Números Complexos
-
- [Números Complexos] Questão envolvendo Potenciação
por everton_stark » Sáb Dez 26, 2015 22:49
- 1 Respostas
- 8730 Exibições
- Última mensagem por rzarour
Sex Abr 01, 2016 07:18
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25
Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.
Caso ainda não tenha dado uma
, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
