teve um dia que eu vi num vídeo que é possivel definir se duas retas são paralelas, concorrentes ou coincidentes a partir da razão dos coeficientes A, B, e C das equações geral da duas reta. Mas não me lembro qual é mesmo a regra para isso.
Se eu nn estiver enganada, se
 =
=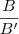 =
=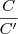 as equações dadas são coincidentes.
as equações dadas são coincidentes.Alguém se lembra desse método e poderia coloca-lo aki, pf?
Obg, Sammy



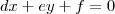

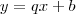
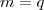 E
E  . Se somente
. Se somente 
 e
e  então, as retas são coincidentes;
então, as retas são coincidentes; , as retas serão paralelas
, as retas serão paralelas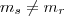 e
e 
