Estou com uma dúvida, em um problema!
Um retângulo tem
![\sqrt[]{12}m](/latexrender/pictures/9ae384aa08395f0e173e5decf86a0c15.png "\sqrt[]{12}m")
de largura e ![\sqrt[]{27}m](/latexrender/pictures/296e8a4f8e791514b4c087988f24b7f2.png "\sqrt[]{27}m")
de comprimento.Qual é a área desse retângulo.Consegui resolver, porém estou com uma dúvida!
![\sqrt[]{12}m . \sqrt[]{27}m = \sqrt[]{12m.27m} = \sqrt[]{324{m}^{2}} = 18m](/latexrender/pictures/71656cd628e93dfce43e8be6ae9a390d.png "\sqrt[]{12}m . \sqrt[]{27}m = \sqrt[]{12m.27m} = \sqrt[]{324{m}^{2}} = 18m")
A resposta no livro é em
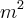, porém a minha resposta é em 
, pois o 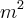, cancela com o índice da raiz! mas como ele pede a área, e área é em 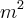, então devo considerar como 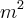, seria isso.
.
: