Sou novo aqui no fórum, e tô tendo dificuldades com a a mati~éria de cálculo na universidade, então vcs vão me ver muito por aqui ;D
A de hj é bem simples:
Determine o domínio da função
![y=\sqrt[2]{\frac{x-1}{7-x}} y=\sqrt[2]{\frac{x-1}{7-x}}](/latexrender/pictures/d6e626f116e738521b151490e2ec678d.png)
O que eu fiz:
1- x deve ser maior ou igual a zero, pois a raiz é par


2 x deve ser maior que zero pois está em uma raiz par e no denominador
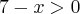


Juntando tudo:
D=[1,7[
E aí, meu raciocínio foi correto?


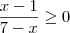 .
. e denominador quando
e denominador quando  .
.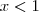 e
e 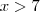 , o que é impossível. Portanto a resposta é
, o que é impossível. Portanto a resposta é  .
.


 .
.



