 por CarolMarques » Qui Mai 03, 2012 20:33
por CarolMarques » Qui Mai 03, 2012 20:33
Olá, Tenho dificuldade na interpretações de problemas sobre conicas como por exemplo este:
O teto de um saguao com 10 m de largura tem a forma de uma semi-elipse com 9 m de altura no centro e 6 m de altura nas paredes laterais.Ache a altura do teto a 2m de cada parede.
Não consigo definir os parametros da elipse.Acredito q pelo menos um deles seja 9.Por favor me ajudem.
-
CarolMarques
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qui Mai 03, 2012 20:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por Russman » Qui Mai 03, 2012 20:39
por Russman » Qui Mai 03, 2012 20:39
Não consegui identificar a forma. ;/
Não tem figura?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por CarolMarques » Qui Mai 03, 2012 21:13
por CarolMarques » Qui Mai 03, 2012 21:13
Não. É só o enunciado =/.
-
CarolMarques
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qui Mai 03, 2012 20:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por Russman » Qui Mai 03, 2012 21:19
por Russman » Qui Mai 03, 2012 21:19
Acho que eu entendi! O teto é como o de uma capela ou abadia. Vou tentar reproduzir aqui e veja se você concorda. Ja posto.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Qui Mai 03, 2012 21:45
por Russman » Qui Mai 03, 2012 21:45
Acho q o esboço problema é este!
- Anexos
-
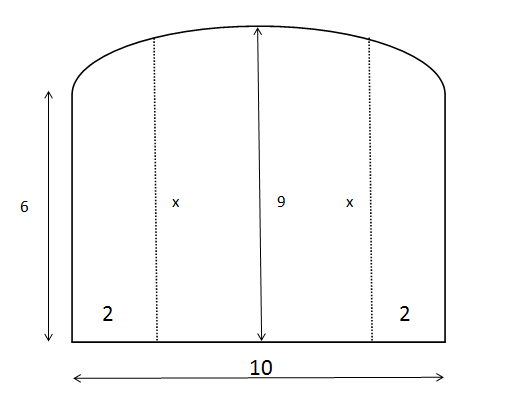
- ScreenHunter_01 May. 03 20.37.gif (6.63 KiB) Exibido 3147 vezes
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Qui Mai 03, 2012 21:58
por Russman » Qui Mai 03, 2012 21:58
Para esta elipse veja que a soma dos semi eixos maiores é 10 e o semi eixo menor é 9-6 = 3. Portanto, chamando de y um eixo vertical e de x( a variável que eu chamei de x vamos trocar para h, ok?) um horizontal, a equação dessa elipse é

.
Assim, para x= -3 ou x = 3 ( que é o equivalente a 2 m das paredes), temos
![\frac{{3}^{2}}{25} + \frac{{y}^{2}}{9} = 1 \Rightarrow y = \pm \sqrt[]{\frac{144}{25}} = \pm \frac{12}{5} = 2,4 \frac{{3}^{2}}{25} + \frac{{y}^{2}}{9} = 1 \Rightarrow y = \pm \sqrt[]{\frac{144}{25}} = \pm \frac{12}{5} = 2,4](/latexrender/pictures/ad45a20828c97341ab49e9edd72af916.png)
.
Portanto,

.
(:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por CarolMarques » Qui Mai 03, 2012 22:06
por CarolMarques » Qui Mai 03, 2012 22:06
É isso mesmo!!Entendi!Muito Obrigadaa!!
-
CarolMarques
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qui Mai 03, 2012 20:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cônicas] duvida.
por Fabricio dalla » Qui Dez 01, 2011 12:32
- 5 Respostas
- 3864 Exibições
- Última mensagem por TheoFerraz

Sex Dez 09, 2011 16:01
Geometria Analítica
-
- [Cônicas] Dúvida exerc. elipse
por MrJuniorFerr » Qua Out 31, 2012 12:58
- 1 Respostas
- 1529 Exibições
- Última mensagem por young_jedi

Qua Out 31, 2012 21:00
Geometria Analítica
-
- Cônicas - Elipse - Só uma dúvida simples
por samra » Sex Jan 24, 2014 01:39
- 2 Respostas
- 1680 Exibições
- Última mensagem por samra

Sex Jan 24, 2014 19:21
Geometria Analítica
-
- Geometria Analítica [Dúvida] sobre cônicas
por pablohas » Sáb Dez 04, 2010 12:55
- 6 Respostas
- 5703 Exibições
- Última mensagem por pablohas

Seg Dez 06, 2010 20:17
Geometria Analítica
-
- [Cônicas]Retas tangentes à cônicas
por Hopkins » Ter Fev 28, 2017 22:39
- 0 Respostas
- 1522 Exibições
- Última mensagem por Hopkins

Ter Fev 28, 2017 22:39
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 .
.![\frac{{3}^{2}}{25} + \frac{{y}^{2}}{9} = 1 \Rightarrow y = \pm \sqrt[]{\frac{144}{25}} = \pm \frac{12}{5} = 2,4 \frac{{3}^{2}}{25} + \frac{{y}^{2}}{9} = 1 \Rightarrow y = \pm \sqrt[]{\frac{144}{25}} = \pm \frac{12}{5} = 2,4](/latexrender/pictures/ad45a20828c97341ab49e9edd72af916.png) .
. .
.