 por Feliperpr » Sáb Abr 21, 2012 16:08
por Feliperpr » Sáb Abr 21, 2012 16:08
Calcule:

, onde C é a curva das equações paramétricas x = a sen (t) ; y = a cos (t); z = a (sen (t) + cos (t), com z maior igual a 0 e menor igual a 2 pi!
Não consegui determinar o parâmetro 'a' e acabei caindo em integral dupla de -y+x+1 dx dy sem conseguir determinar os limites de integração!
Alguém sabe?
-
Feliperpr
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Abr 21, 2012 15:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Russman » Sáb Abr 21, 2012 17:50
por Russman » Sáb Abr 21, 2012 17:50
Feliperpr escreveu:Calcule:

, onde C é a curva das equações paramétricas x = a sen (t) ; y = a cos (t); z = a (sen (t) + cos (t), com z maior igual a 0 e menor igual a 2 pi!
Não consegui determinar o parâmetro 'a' e acabei caindo em integral dupla de -y+x+1 dx dy sem conseguir determinar os limites de integração!
Alguém sabe?
Para tanto é necessário que você faça com que a integral seja efetuada ao longo dos pontos da curva, isto é, substitua as variáveis x,y e z por suas parametrizações!
Desta forma teremos uma integral dependente unicamente do parametro t que, por isso, pode ser calculada. Veja que

utilizando
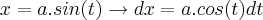
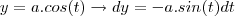

e as identidades trigonométricas

e

.
Agora temos de identificar os limites de integração. Na questão não é o t que varia de 0 a 2pi ?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Sáb Abr 21, 2012 18:51
por Russman » Sáb Abr 21, 2012 18:51
Se t varia de 0 a 2pi, então temos
![\int_{0}^{2\pi} \frac{{a}^{2}}{2}(5cos(2t) -1) =\frac{{a}^{2}}{2}(\frac{5}{2}sin(2t) - t)[t=0,t=2\pi
] =-\pi{a}^{2} \int_{0}^{2\pi} \frac{{a}^{2}}{2}(5cos(2t) -1) =\frac{{a}^{2}}{2}(\frac{5}{2}sin(2t) - t)[t=0,t=2\pi
] =-\pi{a}^{2}](/latexrender/pictures/5b4961bf7472eab8561c677adb5bedc4.png)
Veja que esse processo não é o sugerido pelo Teorema de Stokes! Para tanto é necessário identificar o campo vetorial e a superfície de integração. Fazendo isto você obtem o mesmo resultado. Eu fiz aqui. Se quiser posso postar.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Feliperpr » Sáb Abr 21, 2012 18:54
por Feliperpr » Sáb Abr 21, 2012 18:54
Nossa cara, muito obrigado de verdade!

Se você puder postar, eu agradeço! Mas já me ajudou muito mesmo!

-
Feliperpr
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Abr 21, 2012 15:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Russman » Sáb Abr 21, 2012 19:14
por Russman » Sáb Abr 21, 2012 19:14
O Teorema de Stokes afirma que

que ainda pode ser escrito como

.
Pela integral original vemos que
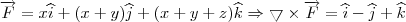

Como convencionamos orientação positiva para fora da superfície de integração usaremos
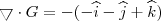
. Assim,

.
(:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Feliperpr » Sáb Abr 21, 2012 19:33
por Feliperpr » Sáb Abr 21, 2012 19:33
Não tenho nem como te agradecer! Muito obrigado mesmo!

-
Feliperpr
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Abr 21, 2012 15:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Teorema de Stokes
por DanielFerreira » Dom Jul 01, 2012 12:07
- 7 Respostas
- 2852 Exibições
- Última mensagem por DanielFerreira

Sáb Jul 07, 2012 20:29
Cálculo: Limites, Derivadas e Integrais
-
- Stokes e divergencia
por Felipe Silva » Ter Jun 08, 2010 18:54
- 0 Respostas
- 971 Exibições
- Última mensagem por Felipe Silva

Ter Jun 08, 2010 18:54
Cálculo: Limites, Derivadas e Integrais
-
- Teorema fundamental do calculo
por Thyago Quimica » Dom Jun 16, 2013 16:38
- 1 Respostas
- 1049 Exibições
- Última mensagem por e8group

Dom Jun 16, 2013 20:12
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Teorema fundamental Calculo
por temujin » Seg Jun 17, 2013 17:36
- 1 Respostas
- 907 Exibições
- Última mensagem por temujin

Seg Jun 17, 2013 19:12
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Calculo de limite usando o teorema do confronto.
por erickm93 » Qua Mai 22, 2013 10:48
- 3 Respostas
- 6019 Exibições
- Última mensagem por erickm93

Qua Mai 22, 2013 23:49
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , onde C é a curva das equações paramétricas x = a sen (t) ; y = a cos (t); z = a (sen (t) + cos (t), com z maior igual a 0 e menor igual a 2 pi!
, onde C é a curva das equações paramétricas x = a sen (t) ; y = a cos (t); z = a (sen (t) + cos (t), com z maior igual a 0 e menor igual a 2 pi!


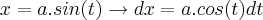
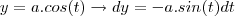

 e
e  .
.
![\int_{0}^{2\pi} \frac{{a}^{2}}{2}(5cos(2t) -1) =\frac{{a}^{2}}{2}(\frac{5}{2}sin(2t) - t)[t=0,t=2\pi
] =-\pi{a}^{2} \int_{0}^{2\pi} \frac{{a}^{2}}{2}(5cos(2t) -1) =\frac{{a}^{2}}{2}(\frac{5}{2}sin(2t) - t)[t=0,t=2\pi
] =-\pi{a}^{2}](/latexrender/pictures/5b4961bf7472eab8561c677adb5bedc4.png)


 .
.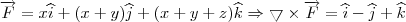

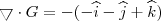 . Assim,
. Assim, .
.![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.