Em uma circunferência de equação x² + y² – 6x – 4y + 9 = 0,
está inscrito um quadrado cujos lados são paralelos aos eixos
cartesianos. A área desse quadrado vale :
Como faço pra achar os vértices do quadrado?




 ( Aqui
( Aqui  foi usado para completar um quadrado perfeito em relação a y )
foi usado para completar um quadrado perfeito em relação a y )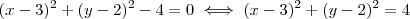 .
.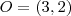 e que o raio é igual a
e que o raio é igual a  .
. .
.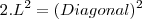 .
. . Note que
. Note que  é a área do quadrado inscrito.
é a área do quadrado inscrito.


Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: