 por Cleyson007 » Sex Abr 13, 2012 23:40
por Cleyson007 » Sex Abr 13, 2012 23:40
Boa noite a todos!
Esboçe a região de integração da seguinte integral iterada

Obs.: Sei resolver a integral iterada em questão encontrando como resposta
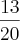
, mas confesso que "peno" no esboço da região de integração.
Alguém pode me explicar de maneira detalhada?
Fico aguardando retorno.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por DanielFerreira » Sex Abr 13, 2012 23:51
por DanielFerreira » Sex Abr 13, 2012 23:51
Cleyson,
costumo resolver daquela forma, veja os intervalos:

e
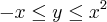
Agora faça um gráfico para:
y = - x
Faça outra para:
y = x²
Junte os dois...
Nesses casos, é fundamental encontrar os pontos de intersecção.
A propósito, como faço p/ postar esses gráficos?
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Sex Abr 13, 2012 23:52
por DanielFerreira » Sex Abr 13, 2012 23:52
também achei
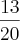
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por MarceloFantini » Sáb Abr 14, 2012 00:08
por MarceloFantini » Sáb Abr 14, 2012 00:08
A equação
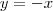
define a bissetriz dos quadrantes pares, portanto é uma reta com coeficiente angular -1. A equação

define a parábola com raíz dupla na origem. Os limites de integração significam que estamos calculando a área desde a reta até a parábola, para

no intervalo
![[0,1] [0,1]](/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png)
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Cleyson007 » Sáb Abr 14, 2012 09:31
por Cleyson007 » Sáb Abr 14, 2012 09:31
Bom dia Danjr5/Fantini!
Observando as informações que recebi montei o gráfico com a região de integração. Segue para avaliação:

Danjr, quanto a postagem dos gráficos utilizo o netUpload (
http://www.netupload.org) para hospedar a imagem e copio o link direto que o site me fornece aqui para o fórum. Tenta aí e, se, surgir dúvida me manda uma mensagem, ok?
Aguardo retorno.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Sáb Abr 14, 2012 11:53
por MarceloFantini » Sáb Abr 14, 2012 11:53
Está correta.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Sáb Abr 14, 2012 11:58
por LuizAquino » Sáb Abr 14, 2012 11:58
danjr5 escreveu: A propósito, como faço p/ postar esses gráficos?
Por favor, vide o tópico:
[Anexos] Envio de anexosviewtopic.php?f=134&t=7460Cleyson007 escreveu:Danjr, quanto a postagem dos gráficos utilizo o netUpload (
http://www.netupload.org) para hospedar a imagem e copio o link direto que o site me fornece aqui para o fórum. Tenta aí e, se, surgir dúvida me manda uma mensagem, ok?
Por favor, evite usar essa estratégia. Tente primeiro anexar o arquivo na sua mensagem (como descrito no tópico indicado acima). Apenas se essa estratégia falhar, daí tente usar essa outra alternativa.
Além disso, eu gostaria de indicar para vocês o programa GeoGebra.
Vide a página oficial desse programa:
http://www.geogebra.org/Se desejar saber como traçar gráficos com o GeoGebra, então basta assistir ao vídeo tutorial "10. Curso de GeoGebra - Funções". Esse vídeo está disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Cleyson007 » Dom Abr 15, 2012 10:48
por Cleyson007 » Dom Abr 15, 2012 10:48
Bom dia!
Luiz Aquino, apenas por curiosidade: Por que deve prevalecer o envio da imagem em anexo? Quando a imagem é carregada na própria página do fórum acaba sobrecarregando algo?
Não entendi...
Aguardo retorno.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Dom Abr 15, 2012 15:17
por MarceloFantini » Dom Abr 15, 2012 15:17
Se estiver anexada ao fórum não corre o risco de se perder. Sites de armazenamento de imagens muitas vezes deletam imagens que são acessadas com pouca frequência como uma forma de liberar espaço, o que não ocorre no fórum.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Cleyson007 » Dom Abr 15, 2012 18:17
por Cleyson007 » Dom Abr 15, 2012 18:17
Boa tarde Fantini!
Obrigado por esclarecer, das próximas vezes anexarei a imagem ao fórum.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral iterada e Região de integração
por Cleyson007 » Sáb Abr 14, 2012 11:21
- 1 Respostas
- 1301 Exibições
- Última mensagem por LuizAquino

Sáb Abr 14, 2012 12:10
Cálculo: Limites, Derivadas e Integrais
-
- Integral iterada e região de integração
por Cleyson007 » Qua Abr 18, 2012 10:59
- 3 Respostas
- 2313 Exibições
- Última mensagem por LuizAquino

Qui Abr 19, 2012 23:15
Cálculo: Limites, Derivadas e Integrais
-
- [Integral dupla]definir região de integração
 por jeferson_justo135 » Qua Jan 14, 2015 21:17
por jeferson_justo135 » Qua Jan 14, 2015 21:17
- 8 Respostas
- 6109 Exibições
- Última mensagem por jeferson_justo135

Seg Fev 09, 2015 17:07
Cálculo: Limites, Derivadas e Integrais
-
- Região de integração
por Cleyson007 » Sex Abr 13, 2012 23:00
- 5 Respostas
- 2457 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 14, 2012 00:19
Cálculo: Limites, Derivadas e Integrais
-
- Região de integração
por Cleyson007 » Qua Abr 18, 2012 11:43
- 1 Respostas
- 1388 Exibições
- Última mensagem por LuizAquino

Qui Abr 19, 2012 14:20
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

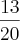 , mas confesso que "peno" no esboço da região de integração.
, mas confesso que "peno" no esboço da região de integração.



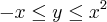

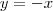 define a bissetriz dos quadrantes pares, portanto é uma reta com coeficiente angular -1. A equação
define a bissetriz dos quadrantes pares, portanto é uma reta com coeficiente angular -1. A equação  define a parábola com raíz dupla na origem. Os limites de integração significam que estamos calculando a área desde a reta até a parábola, para
define a parábola com raíz dupla na origem. Os limites de integração significam que estamos calculando a área desde a reta até a parábola, para  no intervalo
no intervalo ![[0,1] [0,1]](/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) .
.

