Boa Noite!!
Gostaria de tirar uma dúvida, para tirar a raiz quadrada de 13 na mão, estou fazendo com alguns exemplos que eu vi na internet, mas o resultado decimal não é igual ao da calculadora!!! Alguem poderia me dizer onde estou errando!?
sqrt de 13 | 3 => gera 9, sobra 4
-9
4 00 => Aqui já começa o problema, se eu multiplicar utilizando a regra, eu baixo os dois zeros para uma casa decimal e quando multiplico gera 94 * 4 = 376 que iria para 3,4 (o qociente) , mas na calculadora o correto seria [3,6]0555..., só que 96*6 = 576 (que passa de 400).
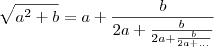
é o maior número inteiro que ao quadrado não supera o radicando.
é o resto obtido entre o radicando e o valor de 
.
mas com apenas duas frações. 
e 
respectivamente. Então:
.
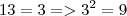Então 3 é o primeiro algarismo da raiz.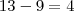
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.