 por Well » Dom Abr 08, 2012 18:42
por Well » Dom Abr 08, 2012 18:42
Estou com dificuldade em usar este teorema
As retas r : ax + by = c e r': a'x + b'y = c' são perpendiculares se,e somente se aa' + bb' = 0
Gostaria de ver a aplicação desse teorema em um problema,isso me ajudaria a entender.
obrigado.
-
Well
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Mar 28, 2012 21:22
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por fraol » Dom Abr 08, 2012 18:59
por fraol » Dom Abr 08, 2012 18:59
Serve um exemplo?
reta

, vetor normal =
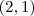
reta

, vetor normal =

r e s são perpendiculares.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Well » Dom Abr 08, 2012 19:25
por Well » Dom Abr 08, 2012 19:25
fraol escreveu:Serve um exemplo?
reta

, vetor normal =
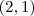
reta

, vetor normal =

r e s são perpendiculares.
é isso mesmo que eu queria.
Mas se eu tenho a reta
r: x + 3y = 1,como faço para achar a reta perpendicular a esta.Usando o teorema que citei.
-
Well
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Mar 28, 2012 21:22
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por fraol » Dom Abr 08, 2012 19:40
por fraol » Dom Abr 08, 2012 19:40
Para
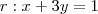
você tem a = 1 e b = 3.
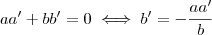
Agora você atribui um valor para a' e acha o b', por exemplo:
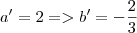
Assim uma possível reta perpendicular é
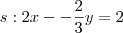
.
Esse último 2 é, relativamente, arbitrário - está relacionado com a interseção da reta com o eixo y.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Well » Dom Abr 08, 2012 20:49
por Well » Dom Abr 08, 2012 20:49
Entendi,muito obrigado!
-
Well
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Mar 28, 2012 21:22
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [RETAS] Descobrir ponto através de retas
 por renan_a » Qui Set 27, 2012 11:10
por renan_a » Qui Set 27, 2012 11:10
- 5 Respostas
- 3094 Exibições
- Última mensagem por renan_a

Sáb Set 29, 2012 18:37
Geometria Analítica
-
- retas
por cristina » Qui Nov 26, 2009 01:01
- 1 Respostas
- 1557 Exibições
- Última mensagem por Neperiano

Sex Set 23, 2011 19:28
Geometria Analítica
-
- Retas
por Jaison Werner » Ter Abr 27, 2010 18:52
- 2 Respostas
- 1820 Exibições
- Última mensagem por Mathmatematica

Dom Jun 13, 2010 01:18
Geometria Analítica
-
- Retas
por manuoliveira » Qua Mai 23, 2012 16:28
- 1 Respostas
- 6880 Exibições
- Última mensagem por LuizAquino

Qua Mai 23, 2012 20:44
Geometria Analítica
-
- [Retas]
por dehcalegari » Seg Jun 24, 2013 17:57
- 2 Respostas
- 1505 Exibições
- Última mensagem por dehcalegari

Ter Jun 25, 2013 15:21
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 , vetor normal =
, vetor normal = 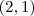
 , vetor normal =
, vetor normal =

, vetor normal =
, vetor normal =

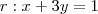 você tem a = 1 e b = 3.
você tem a = 1 e b = 3.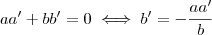
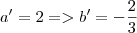
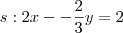 .
.
