O exercício é o seguinte:
Marcando no círculo trigonométrico as extremidades dos arcos da forma
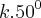 , k inteiro, obtemos os vértices de um polígono regular cujo número de lados é igual a:
, k inteiro, obtemos os vértices de um polígono regular cujo número de lados é igual a: Resposta: 36
Dúvidas:
Meu problema inicial é que não entendi direito o enunciado,
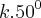 é o comprimento do arco?
é o comprimento do arco?Sei que os lados e os ângulos são congruentes e que
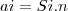

O diâmetro do círculo é a diagonal do polígono?
K seria o raio e
 o
o  ?
?Grata desde já!


 assim:
assim: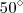 em
em  marcações, teremos um polígono regular de
marcações, teremos um polígono regular de  por
por 
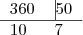
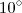 .
. .
. do polígono:
do polígono: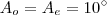
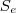 é (I):
é (I):



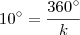
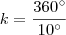
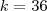

 é um ângulo central da circunferência
é um ângulo central da circunferência  de centro
de centro  .
. : ângulo interno
: ângulo interno

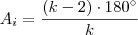
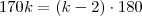

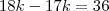
![\frac{\sqrt[]{3}}{2} \frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png) com 0,5 (tanto positivo quando negativo). Já arrumei. Caso alguém tenha baixado, é só baixar o novo arquivo que está corrigido.
com 0,5 (tanto positivo quando negativo). Já arrumei. Caso alguém tenha baixado, é só baixar o novo arquivo que está corrigido.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)