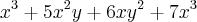 , verfique
, verfique 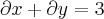 .
.eu consigo fazer a derivada parcial de x e y, mas nao consigo entender como se faz essa parte da verificação . eu tentei derivar em relação a x e y e igualar a 3 . chego até essa parte
 . por favor se puderem me orientar agradeço .
. por favor se puderem me orientar agradeço .
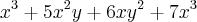 , verfique
, verfique 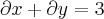 .
. . por favor se puderem me orientar agradeço .
. por favor se puderem me orientar agradeço .
Marcelo_ribeiro escreveu:olá pessoal ... estou com duvida no seguinte exercicio : w= Ln (, verfique
.
Marcelo_ribeiro escreveu:eu consigo fazer a derivada parcial de x e y, mas nao consigo entender como se faz essa parte da verificação.
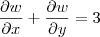 , ele deseja que você faça o seguinte:
, ele deseja que você faça o seguinte:

Marcelo_ribeiro escreveu:olá , aonde tem erro no enunciado?
Marcelo_ribeiro escreveu:w= Ln (, verfique

, verfique
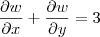
Marcelo_ribeiro escreveu:eu só nao consegui inserir o Ln na fórmula de imagem.
[tex]\ln u[/tex]
Marcelo_ribeiro escreveu:eu somei as derivadas de x e y . e deu aquele resultado que eu mostrei ali em cima, gostaria de saber o que tenho q fazer posteriormente.
Marcelo_ribeiro escreveu:chego até essa parte
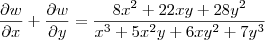

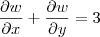 . Em outras palavras, a afirmação feita no exercício é falsa.
. Em outras palavras, a afirmação feita no exercício é falsa.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)