 por Marcelo_ribeiro » Seg Mar 26, 2012 13:57
por Marcelo_ribeiro » Seg Mar 26, 2012 13:57
olá pessoal ... estou com duvida no seguinte exercicio : w= Ln (
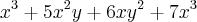
, verfique
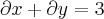
.
eu consigo fazer a derivada parcial de x e y, mas nao consigo entender como se faz essa parte da verificação . eu tentei derivar em relação a x e y e igualar a 3 . chego até essa parte

. por favor se puderem me orientar agradeço .
-
Marcelo_ribeiro
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Mar 26, 2012 13:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: economia
- Andamento: cursando
 por LuizAquino » Seg Mar 26, 2012 15:09
por LuizAquino » Seg Mar 26, 2012 15:09
Marcelo_ribeiro escreveu:olá pessoal ... estou com duvida no seguinte exercicio : w= Ln (
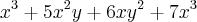
, verfique
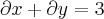
.
Por favor, verifique o enunciado do exercício. Você tem certeza que digitou o enunciado corretamente?
Marcelo_ribeiro escreveu:eu consigo fazer a derivada parcial de x e y, mas nao consigo entender como se faz essa parte da verificação.
Quando ele diz para verificar se
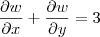
, ele deseja que você faça o seguinte:
1) calcule a derivada parcial de w em relação a x;
2) calcule a derivada parcial de w em relação a y;
3) some essas duas derivadas parciais;
4) agora responda: o resultado dessa soma é igual a 3?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Marcelo_ribeiro » Seg Mar 26, 2012 15:19
por Marcelo_ribeiro » Seg Mar 26, 2012 15:19
olá , aonde tem erro no enunciado ? eu só nao consegui inserir o Ln na fórmula de imagem. mas de resto acho q esta correto . eu somei as derivadas de x e y . e deu aquele resultado que eu mostrei ali em cima, gostaria de saber o que tenho q fazer posteriormente.
-
Marcelo_ribeiro
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Mar 26, 2012 13:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: economia
- Andamento: cursando
 por LuizAquino » Seg Mar 26, 2012 17:09
por LuizAquino » Seg Mar 26, 2012 17:09
Marcelo_ribeiro escreveu:olá , aonde tem erro no enunciado?
Eis o que você escreveu (note as partes em destaque):
Marcelo_ribeiro escreveu:w= Ln (
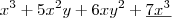
, verfique

Mas eu presumo que o texto original do exercício seja:

, verfique
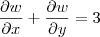
Marcelo_ribeiro escreveu:eu só nao consegui inserir o Ln na fórmula de imagem.
Use um código como:
- Código: Selecionar todos
[tex]\ln u[/tex]
O resultado desse código é:

Marcelo_ribeiro escreveu:eu somei as derivadas de x e y . e deu aquele resultado que eu mostrei ali em cima, gostaria de saber o que tenho q fazer posteriormente.
Eis o que você escreveu:
Marcelo_ribeiro escreveu:chego até essa parte

Ou seja, você está dizendo que:
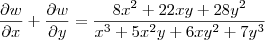
Mas o correto seria (considerando a função w que escrevi acima):

Note que no numerador você escreveu 28y² ao invés de 27y².
Pois bem. Considerando essa expressão para a soma das derivadas parciais, não é possível simplificá-la para obter 3. Isso significa que
não é verdade que
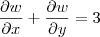
. Em outras palavras, a afirmação feita no exercício é falsa.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Marcelo_ribeiro » Ter Mar 27, 2012 02:28
por Marcelo_ribeiro » Ter Mar 27, 2012 02:28
ah entendi, po vlw pela explicação e pela dica de como inserir ln... brigadão msm !
abraçoo
-
Marcelo_ribeiro
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Mar 26, 2012 13:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: economia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada Parcial de 1ª Ordem] - Derivada parcial num ponto
por Vitor2+ » Dom Jul 01, 2012 16:27
- 6 Respostas
- 4789 Exibições
- Última mensagem por e8group

Seg Jul 02, 2012 10:56
Cálculo: Limites, Derivadas e Integrais
-
- derivada parcial
por jmario » Dom Abr 18, 2010 11:41
- 0 Respostas
- 1796 Exibições
- Última mensagem por jmario

Dom Abr 18, 2010 11:41
Cálculo: Limites, Derivadas e Integrais
-
- Derivada Parcial
por Silva339 » Seg Mar 25, 2013 19:06
- 1 Respostas
- 1933 Exibições
- Última mensagem por DanielFerreira

Sex Mar 29, 2013 02:28
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada Parcial]
por Russman » Qui Mar 28, 2013 22:04
- 1 Respostas
- 1687 Exibições
- Última mensagem por Russman

Sex Mar 29, 2013 13:00
Cálculo: Limites, Derivadas e Integrais
-
- Derivada parcial
por guilherme5088 » Seg Mar 23, 2020 17:55
- 1 Respostas
- 4355 Exibições
- Última mensagem por guilherme5088

Seg Mar 23, 2020 17:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
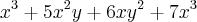 , verfique
, verfique 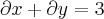 .
. . por favor se puderem me orientar agradeço .
. por favor se puderem me orientar agradeço .
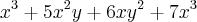 , verfique
, verfique 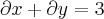 .
. . por favor se puderem me orientar agradeço .
. por favor se puderem me orientar agradeço .
, verfique
.
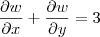 , ele deseja que você faça o seguinte:
, ele deseja que você faça o seguinte:

, verfique

, verfique
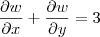

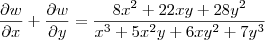

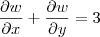 . Em outras palavras, a afirmação feita no exercício é falsa.
. Em outras palavras, a afirmação feita no exercício é falsa.
