 por Cleyson007 » Dom Jun 14, 2009 16:21
por Cleyson007 » Dom Jun 14, 2009 16:21
Olá, boa tarde!
Segue exercício: --> A equação

possui raízes possitivas

e

, cada uma delas com multiplicidade 2. Se

, calcule:
a) A soma das raízes da equação. b) O produto das raízes da equação. c) O valor de m. d) As raízes

e

, se

. e) O valor de n.
Bom, estou resolvendo assim:
Raízes
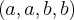

, logo
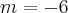
(Pois

) -->
Resposta da letra cComo,

-->

-->
Resposta da letra a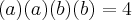
-->
Resposta da letra bComo,


Resolvendo o sistema de equações:

e

-->
Resposta da letra d 
Tenho dúvida na letra e (está havendo divergência entre o gabarito e minha resposta)

Veja meu raciocínio:
 Resolvendo, encontro
Resolvendo, encontro  (O gabarito aponta
(O gabarito aponta  )
)Agradeço sua ajuda.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Cleyson007 » Qua Jun 17, 2009 09:20
por Cleyson007 » Qua Jun 17, 2009 09:20
Bom dia!
Encontrei um erro na minha resolução

Mas minha resposta continua divergindo com a do gabarito

Meu erro está justamente na letra
e...
Eu montei uma equação com três produtos, quando deveria ter sido quatro produtos, pois a equação é de grau 4

Com quatro produtos, a resposta será:

Continuo achando que o gabarito está errado

Alguém pode opinar?
Agradeço sua ajuda.
Um abraço.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação polinomial] Ajuda com essa equação?
por Mkdj21 » Sáb Jan 26, 2013 16:19
- 1 Respostas
- 13017 Exibições
- Última mensagem por young_jedi

Dom Jan 27, 2013 17:15
Equações
-
- Equação Polinomial
por gustavowelp » Dom Jun 27, 2010 11:53
- 3 Respostas
- 3287 Exibições
- Última mensagem por Douglasm

Dom Jun 27, 2010 12:37
Sistemas de Equações
-
- Equação polinomial
por cristina » Sáb Set 18, 2010 17:29
- 5 Respostas
- 4174 Exibições
- Última mensagem por alexandre32100

Sex Set 24, 2010 01:45
Polinômios
-
- (ITA) Equação polinomial
por Carolziiinhaaah » Sex Fev 04, 2011 15:35
- 7 Respostas
- 5924 Exibições
- Última mensagem por Renato_RJ

Qua Fev 16, 2011 00:32
Álgebra Elementar
-
- Equação Polinomial
por Flavio Cacequi » Seg Jun 11, 2018 16:39
- 1 Respostas
- 5033 Exibições
- Última mensagem por DanielFerreira

Sex Set 13, 2019 21:42
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 possui raízes possitivas
possui raízes possitivas  e
e  , cada uma delas com multiplicidade 2. Se
, cada uma delas com multiplicidade 2. Se  , calcule:
, calcule: e
e  , se
, se  . e) O valor de n.
. e) O valor de n.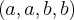
 , logo
, logo 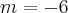 (Pois
(Pois  ) --> Resposta da letra c
) --> Resposta da letra c -->
-->  --> Resposta da letra a
--> Resposta da letra a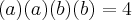 --> Resposta da letra b
--> Resposta da letra b

 e
e  --> Resposta da letra d
--> Resposta da letra d Tenho dúvida na letra e (está havendo divergência entre o gabarito e minha resposta)
Tenho dúvida na letra e (está havendo divergência entre o gabarito e minha resposta) 

 (O gabarito aponta
(O gabarito aponta  )
)







 , avisa que eu resolvo.
, avisa que eu resolvo.

