 por Manuella Vieira » Sex Mar 16, 2012 18:40
por Manuella Vieira » Sex Mar 16, 2012 18:40
Olá, não sei se estou fazendo certo. Descobri o fórum e resolvi tentar =]
Bem, eu estou fazendo cursinho pré-vestibular e já terminei o ensino médio.
Mas não dos detalhes, do que fazer e como.
Eu não faço a minima ideia de como resolve, já tentei e não consigo. ='(
Eu sempre tive dificuldade. Interpretar e resolver.
Esta que eu estou com dificuldade,
não sei o que fazer com o k :/
Deve ser muito fácil. Lá vai:
O menor valor inteiro de k para que a equação algébrica 2x(kx-4)-x²+6=0 em x não tenha raízes reais é:
a) -1 b)2 c)3 d)4 e)5
fico triste por não lembrar :/
eu quero aprender de novo

por favor me ajude!
-
Manuella Vieira
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Mar 16, 2012 18:15
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Sex Mar 16, 2012 19:50
por LuizAquino » Sex Mar 16, 2012 19:50
Manuella Vieira escreveu:O menor valor inteiro de k para que a equação algébrica 2x(kx-4)-x²+6=0 em x não tenha raízes reais é:
a) -1 b)2 c)3 d)4 e)5
Uma equação polinomial do 2º grau tem o formato abaixo:

Para que essa equação não tenha raízes reais, devemos ter
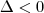
, sendo que

.
A equação do exercício que você postou é:

Podemos arrumar essa equação dessa forma:

Deseja-se então que essa equação polinomial do 2º grau não tenha raízes reais. Sendo assim, temos que deve ocorrer:

Agora tente terminar.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Manuella Vieira » Sex Mar 16, 2012 20:46
por Manuella Vieira » Sex Mar 16, 2012 20:46
LuizAquino escreveu:Podemos arrumar essa equação dessa forma:

Deseja-se então que essa equação polinomial do 2º grau não tenha raízes reais. Sendo assim, temos que deve ocorrer:

Agora tente terminar.
Não entendi o jeito que vc arrumou.
Mas mesmo assim tentei, juro que tentei, tentei mesmo!
Mas não consigo, da fração, da raiz de 32... já deu até 1,83...
Não sei que formula tenho que usar ou como aplicar...
Por favor, não quero ser chata, mas tu sabes algum livro que pode me ajudar? Ou algum site com a matéria explicada desde o inicio?
Muitoooo obrigada pela atenção

-
Manuella Vieira
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Mar 16, 2012 18:15
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Sex Mar 16, 2012 22:26
por MarceloFantini » Sex Mar 16, 2012 22:26
A coleção de livros do Gelson Iezzi chamada "Fundamentos de Matemática Elementar" pode te ajudar. Sobre o que ele fez, sempre que temos uma equação do tipo
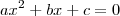
e

é diferente de zero, sabemos que são duas soluções e são da forma
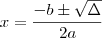
, onde as letras representam os números da equação inicial. Esse símbolo

denota um outro número auxiliar que ajuda a determinar se ela tem soluções
reais ou não.
Quebrando em casos, o valor dele é
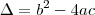
. Se ele for maior que zero, teremos que ela tem duas soluções
diferentes. Se for igual a zero, as duas soluções são iguais. Se for menor que zero, não tem soluções
reais. Ou seja,

tem duas soluções diferentes,

tem duas iguais e
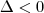
não tem soluções
reais.
Agora tente seguir o que o Luiz disse.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Sáb Mar 17, 2012 22:03
por LuizAquino » Sáb Mar 17, 2012 22:03
Manuella Vieira escreveu:Não entendi o jeito que vc arrumou.
Mas mesmo assim tentei, juro que tentei, tentei mesmo!
Mas não consigo, da fração, da raiz de 32... já deu até 1,83...
Não sei que formula tenho que usar ou como aplicar...
Vejamos onde eu parei:
Continuando, temos que:



"Passando" o -48 dividindo, como esse é um número negativo, devemos inverter o sinal da desigualdade.


Calculando 11/6, obtemos aproximadamente 1,83.
O exercício pede "o menor valor inteiro de k". Então a pergunta é: qual é o menor número inteiro k tal que k > 1,83? Esse número inteiro é o 2. Portanto, temos que k = 2.
Manuella Vieira escreveu:Por favor, não quero ser chata, mas tu sabes algum livro que pode me ajudar? Ou algum site com a matéria explicada desde o inicio?
Além do livro já indicado pelo colega
MarceloFantini, eu recomendo as videoaulas do canal do Nerckie no YouTube. O endereço do canal dele é:
http://www.youtube.com/nerckiePor exemplo, procure pela videoaula "Matemática Zero - Aula 14 - Equação do Segundo Grau".
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Manuella Vieira » Ter Mar 20, 2012 19:30
por Manuella Vieira » Ter Mar 20, 2012 19:30
Muuuuito obrigada!

vou procurar mesmo este livro =D
-
Manuella Vieira
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Mar 16, 2012 18:15
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação do 1º Grau - Como montar a equação
por macedo1967 » Sáb Out 07, 2017 12:53
- 1 Respostas
- 8036 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:17
Equações
-
- [Equação Modular] com equação de 2º grau
por paola-carneiro » Qui Abr 05, 2012 15:53
- 2 Respostas
- 3415 Exibições
- Última mensagem por paola-carneiro

Sex Abr 06, 2012 16:23
Funções
-
- Equação do 1 Grau
por luanxd » Ter Jan 26, 2010 00:06
- 3 Respostas
- 5520 Exibições
- Última mensagem por Cleyson007

Qua Jan 27, 2010 20:40
Polinômios
-
- equação do 2º grau
por juniorthai » Seg Fev 08, 2010 12:05
- 2 Respostas
- 11755 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 06, 2010 20:48
Trigonometria
-
- equação do 2º grau
por juniorthai » Qui Fev 11, 2010 08:15
- 6 Respostas
- 8348 Exibições
- Última mensagem por lulopes

Sex Dez 08, 2017 20:05
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




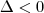 , sendo que
, sendo que  .
.



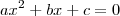 e
e  é diferente de zero, sabemos que são duas soluções e são da forma
é diferente de zero, sabemos que são duas soluções e são da forma 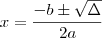 , onde as letras representam os números da equação inicial. Esse símbolo
, onde as letras representam os números da equação inicial. Esse símbolo  denota um outro número auxiliar que ajuda a determinar se ela tem soluções
denota um outro número auxiliar que ajuda a determinar se ela tem soluções 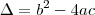 . Se ele for maior que zero, teremos que ela tem duas soluções
. Se ele for maior que zero, teremos que ela tem duas soluções  tem duas soluções diferentes,
tem duas soluções diferentes,  tem duas iguais e
tem duas iguais e 




