O exercício é o seguinte:
O sólido abaixo é composto de dois cubos de arestas 2 cm e 1 cm e centros M e N.
a) Achar a distância AB.
b) Achar a distância MN.
a) Para o AB, eu usei o triângulo ABC que pelo Teorema de Pitágoras:
 =
= +
+
![AB=\sqrt[]{{3}^{2}+{1}^{2}} AB=\sqrt[]{{3}^{2}+{1}^{2}}](/latexrender/pictures/643c9822ee7311c4638264e0fe9d523f.png)
![AB=\sqrt[]{10} AB=\sqrt[]{10}](/latexrender/pictures/018f133de4f87f5fc595f6c2960548de.png) cm
cmb) Para MN, usei o triângulo MNO que pelo Teorema de Pitágoras:

![MN=\sqrt[]{\left(\frac{3}{2} \right)^{2}+\left(\frac{1}{2} \right)^{2}} MN=\sqrt[]{\left(\frac{3}{2} \right)^{2}+\left(\frac{1}{2} \right)^{2}}](/latexrender/pictures/417fe7c0d528d18a01303bfc6e29471e.png)
![MN=\sqrt[]{\frac{9}{4}+\frac{1}{4}} MN=\sqrt[]{\frac{9}{4}+\frac{1}{4}}](/latexrender/pictures/1627dfa5bc6aef4c17f119ce75681c59.png)
![MN=\sqrt[]{\frac{10}{4}} MN=\sqrt[]{\frac{10}{4}}](/latexrender/pictures/d1a74dbcb977325ecb1b3db1722a3917.png)
![MN=\frac{\sqrt[]{10}}{2} MN=\frac{\sqrt[]{10}}{2}](/latexrender/pictures/fb391c288a68df6e5d41cf1c27536035.png) cm
cmDe acordo com o livro, as respostas são:
a)
![AB=\sqrt[]{10} AB=\sqrt[]{10}](/latexrender/pictures/018f133de4f87f5fc595f6c2960548de.png) cm
cmb)
![MN=\frac{\sqrt[]{11}}{2} MN=\frac{\sqrt[]{11}}{2}](/latexrender/pictures/bff70868a93119771a2d0e9b7773d684.png) cm
cmEntão, queria saber se fui eu que errei ou se a resposta do livro que está errada.
Mais uma vez grata.
Praticamente uma pergunta por dia...




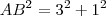

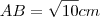
 Está no centro “levitando”, ou seja, a uma altura do cubo menor de
Está no centro “levitando”, ou seja, a uma altura do cubo menor de 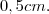
 Sofre o mesmo processo de “levitar”, estando a uma altura de
Sofre o mesmo processo de “levitar”, estando a uma altura de 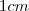 em relação a sua base.
em relação a sua base. se N estivesse, precisamente sobre
se N estivesse, precisamente sobre 
 da aresta e ao chegar se deslocaria para direita em direção a
da aresta e ao chegar se deslocaria para direita em direção a 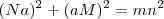
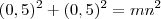
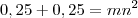
 , intencionalmente paramos aqui.
, intencionalmente paramos aqui. 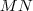 no espaço:
no espaço: , substituindo...
, substituindo...  (percebeu porque não extraí a raiz).
(percebeu porque não extraí a raiz).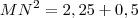
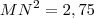
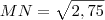 , decompondo
, decompondo 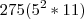 e
e 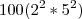
 ,simplificando e extraindo a raiz quadrada
,simplificando e extraindo a raiz quadrada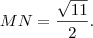




 , avisa que eu resolvo.
, avisa que eu resolvo.

