 por Danilo » Sáb Mar 17, 2012 10:39
por Danilo » Sáb Mar 17, 2012 10:39
Decida se as proposições a seguir são verdadeira ou falsa.
Proposição 1: Se x é um número real positivo, então (?x)² = x Proposição 2: Se x é um número real positivo, então (?-x)² = - x Proposição 3: Se x é um número real, então ?x² = x
Galera, eu sei que, se existir contra-exemplo para a proposição, a mesma é falsa. E posso dar valor para quantos ''xizes'' eu quiser (pelo menos para a proposição 1) , que isso não é suficiente para que a proposição seja verdadeira. Então basta eu provar que a proposição não admite contra-exemplos. Bom, qual é o melhor caminho que eu devo seguir? Não vejo como demonstrar, ou provar que a(s) proposição não existe/existe contra-exemplo. Muito grato se puderem clarear a minha mente. Obrigado.
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por fraol » Sáb Mar 17, 2012 11:27
por fraol » Sáb Mar 17, 2012 11:27
Creio que o melhor caminho a seguir varia de caso para caso. Em geral, o que se pode fazer é analisar as possibilidades que temos para tentar a demonstração e então escolher um caminho. Se não sair por esse caminho, então tentamos um outro. Com o tempo e a prática os melhores caminhos vão ficando mais claros.
Quando temos uma expressão do tipo

para provar uma alternativa seria tentar provar por contradição, isto é afirmamos que

e desenvolvemos essa expressão, então se chegarmos a uma contradição concluímos que

.
Há um tempo atrás, traduzi um artigo em
http://acontanaobate.blogspot.com.br/2011/07/recomendacoes-para-estudantes.html que trata de várias alternativas de demonstração de sentenças matemáticas. Se tiver um tempinho dá uma olhada lá.
Grato.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Danilo » Sáb Mar 17, 2012 11:33
por Danilo » Sáb Mar 17, 2012 11:33
Sim, Fraol, é verdade. Posso tentar demontrar por absurdo. Vou tentar fazer o que você disse, e vou ler o artigo também. E sim, clareou bastante ^^. Obrigado.
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Sáb Mar 17, 2012 15:00
por MarceloFantini » Sáb Mar 17, 2012 15:00
Vale lembrar que raíz quadrada está definida apenas valores positivos. Logo, a primeira com certeza é verdadeira. A segunda segue analogamente. Uma dica para a terceira é: pense no caso em que x for negativo, assumindo que a expressão é

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Danilo » Dom Mar 18, 2012 01:40
por Danilo » Dom Mar 18, 2012 01:40
Pessoal, posso responder dizendo, que, para a proposição - Se x é um número real positivo, então (?x)² -
A proposição não admite contra-exemplo pois, por definição não existe conjunto fora dos reais positivos que satisfaça a proposição. Posso dizer assim? Só preciso dizer se é verdadeiro ou falso e justificar.
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Dom Mar 18, 2012 02:24
por MarceloFantini » Dom Mar 18, 2012 02:24
Cuidado: a expressão

é diferente de
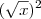
. A primeira admite qualquer número real, a segunda pressupõe que seja não-negativo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Danilo » Dom Mar 18, 2012 10:27
por Danilo » Dom Mar 18, 2012 10:27
bom, então para a primeira, posso dizer: por definição não existe conjunto fora dos reais positivos que satisfaça a proposição. Posso dizer assim?
para a segunda: a proposição é falsa, porque por exemplo temos que se x = -3 (?-3²) = - 3 o que contraria a definição, pois a raiz quadrada de um número é definida apenas para números positivos.
Estou perguntando antes porque é uma uma lista de exercícios que tenho que entregar amanhã :P
correto?
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Dom Mar 18, 2012 14:33
por MarceloFantini » Dom Mar 18, 2012 14:33
Diga que apenas os números reais positivos satisfazem a proposição, sobre o segundo você errou:

. Se fosse -3, a proposição seria correta.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Danilo » Dom Mar 18, 2012 15:33
por Danilo » Dom Mar 18, 2012 15:33
A tá... na verdade o número todo é x². considerei apenas o x... obrigado!!!
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Exercicios básicos
por Martinele » Ter Out 29, 2013 22:24
- 0 Respostas
- 1718 Exibições
- Última mensagem por Martinele

Ter Out 29, 2013 22:24
Geometria Espacial
-
- problemas básicos e sem solução...
por andrellhacker » Qua Ago 19, 2009 22:39
- 9 Respostas
- 8152 Exibições
- Última mensagem por bajinho

Sáb Jul 28, 2012 09:28
Álgebra Elementar
-
- Problema - conceitos básicos da álgebra
por Jacki81 » Qui Fev 25, 2016 18:09
- 0 Respostas
- 1577 Exibições
- Última mensagem por Jacki81

Qui Fev 25, 2016 18:09
Álgebra Elementar
-
- Dúvidas sobre alguns conceitos básicos
por Danilo » Qui Mar 15, 2012 23:53
- 2 Respostas
- 1605 Exibições
- Última mensagem por Danilo

Sex Mar 16, 2012 09:57
Álgebra Elementar
-
- Dúvida em exercício de PAG!
 por Fernanda » Qui Jul 03, 2008 18:20
por Fernanda » Qui Jul 03, 2008 18:20
- 11 Respostas
- 10092 Exibições
- Última mensagem por admin

Sex Jul 04, 2008 05:01
Sequências
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 para provar uma alternativa seria tentar provar por contradição, isto é afirmamos que
para provar uma alternativa seria tentar provar por contradição, isto é afirmamos que  e desenvolvemos essa expressão, então se chegarmos a uma contradição concluímos que
e desenvolvemos essa expressão, então se chegarmos a uma contradição concluímos que  .
.

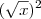 . A primeira admite qualquer número real, a segunda pressupõe que seja não-negativo.
. A primeira admite qualquer número real, a segunda pressupõe que seja não-negativo. . Se fosse -3, a proposição seria correta.
. Se fosse -3, a proposição seria correta.

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.