 por strikeeagle » Seg Mar 12, 2012 10:14
por strikeeagle » Seg Mar 12, 2012 10:14
Amigos, gostaria de ajuda para resolver a seguinte questão:
As seis faces de um dado são equiprováveis e estão marcadas com 1, 2, A, 4, B, C. Lançando simultaneamente dois desses dados, a probabilidade de obtermos na dupla de resultados pelo menos um número par, ou pelo menos uma consoante, é igual a:
A) 7/9
B) 4/5
C) 5/6
D) 8/9
E) 17/18
O gabarito dá a alternativa B, mas não entendi como chegar nisso.
Como no primeiro lançamento teríamos que obter um número par dentre os dois existentes ou uma consoante dentre as duas existentes, logo imaginei que essa probabilidade seria de 4/6. O mesmo vale para o segundo lançamento, então pensei que teríamos outra probabilidade de 4/6 no segundo dado. Depois, como ele pede OU uma coisa OU outra, eu imaginei que bastaria somar as duas probabilidades. Enfim, acabei tentando de várias outras formas, mas não consigo chegar nesses 4/5 de forma alguma. Se alguém puder me dar uma luz, agradeço!

[]s a todos!
-
strikeeagle
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Mar 12, 2012 09:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnólogo em Análise de Sistemas
- Andamento: formado
 por LuizAquino » Seg Mar 12, 2012 19:01
por LuizAquino » Seg Mar 12, 2012 19:01
strikeeagle escreveu:As seis faces de um dado são equiprováveis e estão marcadas com 1, 2, A, 4, B, C. Lançando simultaneamente dois desses dados, a probabilidade de obtermos na dupla de resultados pelo menos um número par, ou pelo menos uma consoante, é igual a:
A) 7/9
B) 4/5
C) 5/6
D) 8/9
E) 17/18
strikeeagle escreveu:O gabarito dá a alternativa B, mas não entendi como chegar nisso.
Como no primeiro lançamento teríamos que obter um número par dentre os dois existentes ou uma consoante dentre as duas existentes, logo imaginei que essa probabilidade seria de 4/6. O mesmo vale para o segundo lançamento, então pensei que teríamos outra probabilidade de 4/6 no segundo dado. Depois, como ele pede OU uma coisa OU outra, eu imaginei que bastaria somar as duas probabilidades. Enfim, acabei tentando de várias outras formas, mas não consigo chegar nesses 4/5 de forma alguma. Se alguém puder me dar uma luz, agradeço!

[]s a todos!
Os dados são lançados simultaneamente e eles não são distinguíveis. Desse modo, o resultado (1, 2) é o mesmo que (2, 1).
Os possíveis resultados para o lançamento estão listados abaixo. Em destaque, temos as possibilidades desejadas.
(1, 1),
(1, 2),
(1, 4), (1, A),
(1, B),
(1, C)(2, 2),
(2, 4),
(2, A),
(2, B),
(2, C)(4, 4),
(4, A),
(4, B),
(4, C)(A, A),
(A, B),
(A, C)(B, B),
(B, C)(C, C)Temos então que:
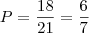
Note que não há essa alternativa entre as opções. Desse modo, todas as alternativas estão erradas.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por strikeeagle » Ter Mar 13, 2012 16:30
por strikeeagle » Ter Mar 13, 2012 16:30
Luiz, obrigado pela resposta.
Confesso ter ficado revoltado por nenhuma alternativa estar correta. De qualquer forma não teria chegado ao número que você chegou, mas perdi muito tempo tentando entender a resposta que o gabarito dava como correta.
Agradeço muito!
Grande abraço!
-
strikeeagle
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Mar 12, 2012 09:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnólogo em Análise de Sistemas
- Andamento: formado
 por strikeeagle » Qui Mar 22, 2012 22:57
por strikeeagle » Qui Mar 22, 2012 22:57
Luiz e demais amigos do fórum, boa noite,
Venho reabrir essa questão, pelo seguinte motivo: ela caiu num concurso recente realizado por uma grande instituição e eu participei dessa prova. Não consegui resolvê-la no dia da aplicação, cheguei em casa e também não consegui resolver. O meu raciocínio seguia um caminho parecido com o do amigo Luiz, mas não o terminei exatamente por perceber que não daria nenhuma das alternativas.
Eu imaginei que havia algo errado com ela, mas não estava seguro para entrar com recurso pedindo a anulação da mesma. Quando você postou a solução e vi que ela seguia um caminho coerente do meu ponto de vista, entrei com o recurso, no entanto, após análise, eles indeferiram, alegando que a alternativa correta é a D mesmo.
Você (Luiz) ou algum outro amigo do fórum sabe como chegar nela? A curiosidade em entendê-la está tão grande que é quase uma questão de vida ou morte.

Se alguém puder ajudar, agradeço.
[]s
-
strikeeagle
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Mar 12, 2012 09:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnólogo em Análise de Sistemas
- Andamento: formado
 por fraol » Qui Mar 22, 2012 23:49
por fraol » Qui Mar 22, 2012 23:49
Minha sugestão é você pensar esse problema pela análise do evento complementar:
Eventos que não interessam: {IMPAR, IMPAR} e {IMPAR, VOGAL}, {VOGAL, IMPAR}, {VOGAL, VOGAL} = 4/36
A probabilidade então é 1 - 4/36 = 32/36 = 8/9.
Na abordagem anterior, contou-se, por exemplo, (A,B) mas não contou (B,A). Contudo esse, assim como outros eram resultados possíveis que atendem as premissas.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por LuizAquino » Sex Mar 23, 2012 08:45
por LuizAquino » Sex Mar 23, 2012 08:45
strikeeagle escreveu:Quando você postou a solução e vi que ela seguia um caminho coerente do meu ponto de vista, entrei com o recurso, no entanto, após análise, eles indeferiram, alegando que a alternativa correta é a D mesmo.
O fato deles indeferirem o seu recurso não significa que eles estão certos.
fraol escreveu:Na abordagem anterior, contou-se, por exemplo, (A,B) mas não contou (B,A). Contudo esse, assim como outros eram resultados possíveis que atendem as premissas.
Note que os dois dados são
iguais e são lançados
simultaneamente.
Desse modo,
não é possível distinguir o resultado (A, B) do resultado (B, A).
Para poder distinguir esses dois resultados, deveria haver uma ordem estabelecida ou ainda alguma diferença entre os dados (por exemplo, a cor). Entretanto, nada disso foi especificado no enunciado do exercício.
Portanto, eu continuo defendendo a minha resolução.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por strikeeagle » Sáb Mar 24, 2012 14:09
por strikeeagle » Sáb Mar 24, 2012 14:09
Amigo fraol, obrigado pela explicação. De fato sua resposta é a que a organizadora da prova gostaria e, como citei anteriormente, eu não teria conseguido chegar nisso sozinho.
Agradeço muito!
No entanto, ao amigo Luiz só tenho a dizer que continuo concordando com seu raciocínio. O enunciado é muito claro quando diz que os dados são iguais e lançados simultaneamente, portanto resultados como (2,1) e (1,2) não podem ser diferenciados. Enfim, agradeço muito aos dois. Acho que foi uma questão infeliz, mas como a empresa que elaborou a prova não deu o braço a torcer, deixemos como está. De qualquer forma acho que as discussões foram válidas e acrescentaram, que é o objetivo do fórum.

[]s a todos!
-
strikeeagle
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Mar 12, 2012 09:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnólogo em Análise de Sistemas
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [probabildade] lançamento de dados
por santtus » Sáb Fev 16, 2013 03:38
- 6 Respostas
- 3414 Exibições
- Última mensagem por DanielFerreira

Dom Fev 17, 2013 17:39
Probabilidade
-
- Lançamento de uma bola
por Cleyson007 » Sex Nov 09, 2012 20:25
- 2 Respostas
- 1845 Exibições
- Última mensagem por Cleyson007

Sex Nov 09, 2012 22:44
Física
-
- Lançamento de dado
por Ana Maria da Silva » Sáb Mar 22, 2014 20:04
- 2 Respostas
- 4253 Exibições
- Última mensagem por paulo testoni

Dom Jun 29, 2014 00:07
Probabilidade
-
- Probabilidade (Lançamento de dado)
por tan lopes » Qui Out 25, 2012 17:06
- 2 Respostas
- 2660 Exibições
- Última mensagem por tan lopes

Ter Out 30, 2012 16:37
Probabilidade
-
- [Lançamento de moedas] Probabilidade
por analuzia » Qua Nov 07, 2012 16:33
- 2 Respostas
- 2903 Exibições
- Última mensagem por analuzia

Qua Nov 07, 2012 17:04
Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



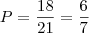





 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.





 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo: