
Resultado deu:
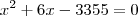
grato
vinirfb


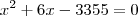


 toda esssa equação dividida por 2
toda esssa equação dividida por 2
ViniRFB escreveu:Pessoal como eu faço essa resolução. Estou com dúvida a respeito qual número é multiplicado por tal número.
Resultado deu:
grato
vinirfb
ViniRFB escreveu:Quero saber o valor de:
toda esssa equação dividida por 2
Quero o passo a passo. Qual ordem que devo proceder? Por favor.
Não sei colocar à questão como ela está realmente por causa dessas benditas fórmulas, mas acho que agora ficou mais claro.
Se possível quando vier a resposta a pessoa possa colocar a equação como deveria ter sido colocada por mim. Que depois eu pego o modelo e nas próximas faço correto!
grato
Vini!!
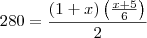



Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)