 por ViniRFB » Sáb Mar 10, 2012 14:05
por ViniRFB » Sáb Mar 10, 2012 14:05
Pessoal como eu faço essa resolução. Estou com dúvida a respeito qual número é multiplicado por tal número.

Resultado deu:
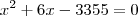
grato
vinirfb
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ViniRFB » Sáb Mar 10, 2012 15:14
por ViniRFB » Sáb Mar 10, 2012 15:14
Quero saber o valor de:


toda esssa equação dividida por 2
Quero o passo a passo. Qual ordem que devo proceder? Por favor.
Não sei colocar à questão como ela está realmente por causa dessas benditas fórmulas, mas acho que agora ficou mais claro.
Se possível quando vier a resposta a pessoa possa colocar a equação como deveria ter sido colocada por mim. Que depois eu pego o modelo e nas próximas faço correto!
grato
Vini!!
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ant_dii » Sáb Mar 10, 2012 15:41
por ant_dii » Sáb Mar 10, 2012 15:41
ViniRFB escreveu:Pessoal como eu faço essa resolução. Estou com dúvida a respeito qual número é multiplicado por tal número.

Resultado deu:
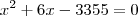
grato
vinirfb
ViniRFB escreveu:Quero saber o valor de:


toda esssa equação dividida por 2
Quero o passo a passo. Qual ordem que devo proceder? Por favor.
Não sei colocar à questão como ela está realmente por causa dessas benditas fórmulas, mas acho que agora ficou mais claro.
Se possível quando vier a resposta a pessoa possa colocar a equação como deveria ter sido colocada por mim. Que depois eu pego o modelo e nas próximas faço correto!
grato
Vini!!
O correto então, é
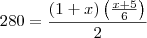
Siga o que pode ser feito
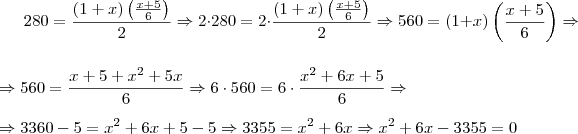
Editado pela última vez por
ant_dii em Sáb Mar 10, 2012 15:49, em um total de 1 vez.
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por ViniRFB » Sáb Mar 10, 2012 15:49
por ViniRFB » Sáb Mar 10, 2012 15:49
Muito Obrigado. ant_dii
Valeu
ViniRFB
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ant_dii » Sáb Mar 10, 2012 15:51
por ant_dii » Sáb Mar 10, 2012 15:51
Que isso...
Disponha
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral da soma/Soma das Integrais.
por Sobreira » Ter Abr 30, 2013 17:41
- 0 Respostas
- 2098 Exibições
- Última mensagem por Sobreira

Ter Abr 30, 2013 17:41
Cálculo: Limites, Derivadas e Integrais
-
- Soma de PG
por a_guia » Seg Jan 04, 2010 22:19
- 1 Respostas
- 2028 Exibições
- Última mensagem por Molina

Seg Jan 04, 2010 22:54
Progressões
-
- Soma
por manuoliveira » Dom Mai 30, 2010 18:23
- 1 Respostas
- 8384 Exibições
- Última mensagem por Douglasm

Dom Mai 30, 2010 20:08
Binômio de Newton
-
- SOMA DE PA
por cristiano » Seg Mai 16, 2011 16:18
- 1 Respostas
- 1686 Exibições
- Última mensagem por Molina

Seg Mai 16, 2011 20:44
Progressões
-
- SOMA DE UMA PA
por silvia fillet » Qua Fev 15, 2012 19:50
- 1 Respostas
- 1830 Exibições
- Última mensagem por silvia fillet

Sáb Fev 18, 2012 11:24
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

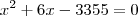


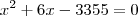


 toda esssa equação dividida por 2
toda esssa equação dividida por 2

toda esssa equação dividida por 2
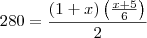
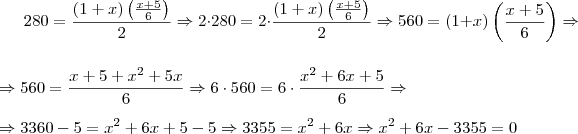





 , avisa que eu resolvo.
, avisa que eu resolvo.

